bribe

Doi oameni pe care, pentru a le păstra anonimitatea, îi vom numi Costel si Costin, participă la lotul de informatică. Costel face parte din comisie, în timp ce Costin este concurent.

Cei doi au făcut o înţelegere cel puţin bizară: contra unor foloase materiale, Costel îl va ajuta pe Costin să obţină $100$ de puncte la una dintre probleme. Stiind că toate problemele de la lot au ca output un singur număr, Costin a ales deja $50$ de numere preferate $R_i$, pe care i le-a transmis lui Costel. Acesta trebuie acum ca, pentru o problemă, să genereze $50$ de teste pentru care răspunsurile sunt cele $50$ de numere alese de Costin.

Problema aleasă de Costel pentru a pune în aplicare planul este următoarea: “Se dă un arbore (graf conex neorientat aciclic) format din $N$ noduri, $1 \leq N \leq 400$. Pentru acesta, se cere să se determine câte mulţimi maxime de noduri independente există pentru arborele dat. O mulţime maximă de noduri independente se definește ca fiind o mulţime de noduri cu cardinal maxim, astfel încât nu există două noduri în mulţime care să fie unite de o muchie din arborele original.”

Din cauza unui accident nefericit care îl împiedică să mai continue, Costel v-a însărcinat pe voi să continuati planul. Construiti $50$ de arbori pentru care, pentru fiecare arbore $i$, răspunsul la problema aleasă este numărul $R_i$.

Restricții și precizări

Această problemă este output-only. Prin urmare, nu trebuie să încărcați o sursă care să afișeze răspunsul. Veți încărca direct fișierele de ieșire corespunzătoare celor de intrare aflate pe interfața de evaluare. Fiecare fișier de intrare are următorul format:

• linia $i \ (1 \leq i \leq 50)$: $R_i$, un număr întreg pozitiv, ($1 \leq R_i \leq 10^{18}$), reprezentând răspunsul dorit pentru testul cu numărul $i$.

În fișierul de ieșire corespunzător trebuie să afișați forma a $50$ de arbori, astfel încât pentru arborele cu numărul $i$ răspunsul la problema propusă de Costel este $R_i$. Arborii vor fi afișați secvențial în fișierul de ieșire. Un arbore individual va fi afișat în următorul mod:

• linia $1$: un număr întreg $N$, $1 \leq N \leq 400$, reprezentând dimensiunea arborelui.
• linia $2 + i$ ($0 \leq i \leq N - 2$): $a$, $b$ două numere întregi $0 \leq a, b \leq N - 1$ ($a \neq b$), semnificând existența unei muchii între nodurile $a$ și $b$.

Se garantează că există soluție pentru toate testele.

Punctare

Pentru un test punctajul maxim se obtine dacă pentru fiecare din cei $50$ de arbori, răspunsul la problema propusă de Costel corespunzător arborelui $i$ este $R_i$. În plus, fiecare arbore afișat în fișierul de intrare trebuie să conțină cel mult $400$ de noduri.

Subtask 1 (13 puncte)

• $1 \leq R_i \leq 20$

Subtask 2 (6 puncte)

• $1 \leq R_i \leq 100$

Subtask 3 (5 puncte)

• $1 \leq R_i \leq 200$

Subtask 4 (7 puncte)

• $1 \leq R_i \leq 10^{18}$
• $R_i$ este putere a lui $2$

Subtask 5 (50 puncte)

• $1 \leq R_i \leq 2 \cdot 10^9$

Subtask 6 (19 puncte)

• $1 \leq R_i \leq 10^{18}$

Exemplu

Intrare

3
2

Ieșire

7
0 1
0 2
2 3
1 4
4 5
4 6
8
0 1
0 2
0 3
3 4
5 4
5 6
5 7

Explicație

Acest exemplu are doar rol demonstrativ întrucât conține doar $2$ numere în fișierul de intrare. Testele oficiale conțin câte $50$ de numere fiecare.

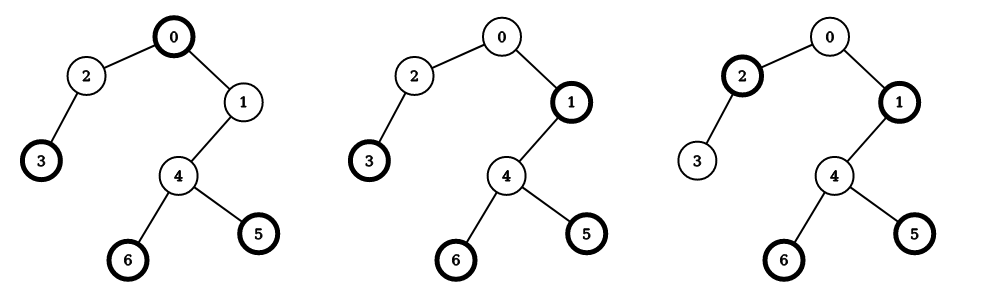
Pentru primul exemplu, trebuie generat un arbore care are exact $3$ mulțimi de noduri independente. Pentru arborele generat, cele $3$ mulțimi posibile care pot fi alese sunt cele din imaginile următoare (nodurile unei mulțimi fiind cele cu marginea ingroșată):