echilateral

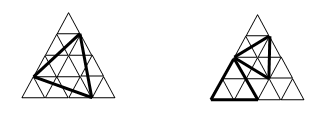
O rețea triunghiulară de latură $n$ se obține descompunând un triunghi echilateral de latură $n$ în triunghiuri echilaterale de latură $1$, folosind drepte paralele la laturile triunghiului inițial. De exemplu în figurile de mai jos avem rețele triunghiulare de latură $4$. Numim noduri ale rețelei vârfurile triunghiurilor de latură $1$ folosite în descompunere. Astfel pe prima rețea am desenat un triunghi echilateral cu vârfuri în nodurile rețelei iar pe a doua rețea am desenat două triunghiuri echilaterale cu vârfuri în noduri.

Cerinţă

Să se scrie un program care pentru $n$, $a$, și $b$ cunoscute, determină numărul de triunghiuri echilaterale cu vârfurile în nodurile unei rețele de latură $n$ care au lungimile laturilor cuprinse între valorile $a$ și $b$.

Date de intrare

Fişierul de intrare echilateral.in conţine pe prima linie numerele $n$, $a$ și $b$ separate prin câte un spaţiu.

Date de ieşire

Fişierul de ieşire echilateral.out va conţine pe prima linie numărul de triunghiuri echilaterale cu vârfurile în nodurile unei rețele de latură $n$ care au lungimile laturilor cuprinse între valorile $a$ și $b$, modulo $666 \ 013$.

Restricţii şi precizări

• $1 \leq n \leq 10^9$;
• $1 \leq a \leq b \leq 10^6$;

Exemplu

echilateral.in

4 1 2

echilateral.out

29

Explicație

Avem $16$ triunghiuri de latură $1$ (cele care acoperă rețeaua).
Mai avem încă $6$ triunghiuri de latură $\sqrt{3}$ (similar triunghiului din a doua figură și având una dintre laturi verticală).
Mai avem încă $7$ triunghiuri de latură $2$.
În total avem $16+6+7=29$ triunghiuri.