galax

Într-un viitor mai mult sau mai puţin apropiat, oamenii vor popula $n$ galaxii, numerotate de la $1$ la $n$. Datorită dezvoltării tehnologiei de transport spaţial este posibil ca din oricare galaxie să se ajungă printr-un zbor în oricare altă galaxie. Fiecare pereche de galaxii defineşte astfel un zbor care poate fi parcurs în orice sens.

La un moment dat se ia hotărârea ca $\frac{n+1}{2}$ companii de transport să asigure libera circulaţie a oamenilor între galaxiile existente. Companiile sunt numerotate de la $1$ la $\frac{n+1}{2}$. Fiecărei companii $x$ i se va atribui o mulţime de zboruri $Z_x$. Notăm cu $G_x$ mulţimea galaxiilor deservite de compania $x$ prin zborurile din mulţimea $Z_x$.

Zborurile vor fi distribuite conform următoarelor reguli:

1. prin zborurile din $Z_x$, compania $x$ poate transporta oameni între oricare două galaxii din $G_x$, (fie direct, fie trecând prin alte galaxii din $G_x$);
2. pentru oricare două galaxii din $G_x$, modul în care compania $x$ transportă călătorii de la o galaxie la cealaltă este unic;
3. fiecare zbor trebuie să fie atribuit exact unei singure companii.

Cerinţă

Scrieţi un program care să determine o modalitate de atribuire a zborurilor celor $\frac{n+1}{2}$ companii în conformitate cu regulile enunţate mai sus.

Date de intrare

Fişierul de intrare galax.in conţine o singură linie pe care va fi scris un număr natural $n$, reprezentând numărul de galaxii.

Date de ieşire

Fişierul de ieşire galax.out va conţine câte o linie pentru fiecare pereche de galaxii. Pe această linie vor fi scrise $3$ numere naturale $a \ b \ c$, cu semnificaţia “zborul dintre galaxiile $a$ şi $b$ este atribuit companiei $c$”.

Restricții și precizări

• $3 < n < 1 \ 001$
• $a \ div \ b$ este câtul împărţirii întregi a lui $a$ la $b$.

Exemplul 1

galax.in

4

galax.out

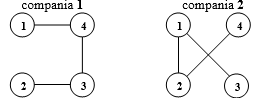
1 4 1
1 2 2
4 3 1
3 1 2
3 2 1
2 4 2

Explicație

Exemplul 2

galax.in

5

galax.out

1 2 1
1 5 3
2 4 1
4 3 1
5 3 1
1 3 2
2 3 2
1 4 3
5 2 2
5 4 2

Explicație