Un arbore binar este un arbore cu rădăcină în care fiecare nod are maxim $2$ fii. Un arbore binar de căutare (Binary Search Tree) este un arbore binar în care fiecare nod are asociată o valoare, iar valoarea unui nod este strict mai mare decât toate valorile din subarborele său stâng și strict mai mică decât toate valorile din subarborele său drept. Un exemplu de arbore binar de căutare este cel din stânga iar unul greșit în dreapta (deoarece $9$ se află în subarborele stâng al lui $5$ şi $3$).

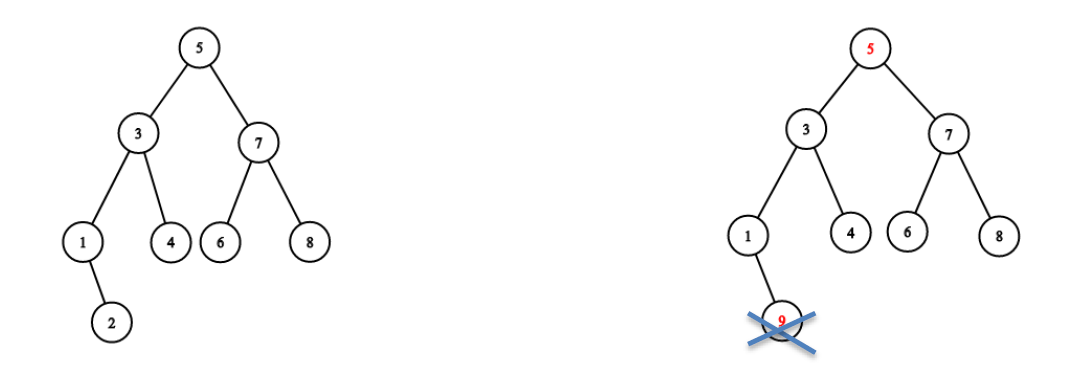
Cerinţă

Cunoscând numerele naturale $N$, $K$ şi un şir $A_1, A_2, ..., A_K$ cu toate elementele numere naturale distincte nenule mai mici sau egale cu $N$, vi se cere să numărați câți arbori binari de căutare există cu $N$ noduri având valorile asociate nodurilor $1, 2, ..., N$ (în orice ordine validă), astfel încât şirul $A_1, A_2, ..., A_K$ să formeze un lanț în arbore în această ordine. De exemplu, pentru $N=8$, $K=5$, $A=(6, 7, 5, 3, 4)$, arborele de mai sus din stânga este unul valid.

Date de intrare

Fișierul de intrare countbst.in va conține pe prima linie un număr natural $T$ (numărul de teste), urmat de $T$ teste. Fiecare test va fi descris prin două linii:

• Pe prima linie se vor găsi două numere naturale $N$ și $K$ separate printr-un spaţiu.
• Pe linia a doua se vor găsi cele $K$ numere naturale nenule distincte $A_1, A_2, ..., A_K$ separate şi urmate de un spaţiu.

Date de ieşire

Fișierul de ieșire countbst.out va conține răspunsurile pentru fiecare dintre cele $T$ teste, câte unul pe linie: numărul de arbori binari de căutare ce conțin șirul de $K$ numere ca lanț, afișat modulo $1\ 000\ 000\ 007$ în ordinea testelor din fişierul de intrare.

Restricţii

• $N \leq 3\ 000\ 000$
• $\sum K \leq 200\ 000$
• $T \leq 200\ 000$

Subtask 0 (3 puncte)

• $N \leq 12$
• $K \leq N$
• $T \leq 10$

Subtask 1 (4 puncte)

• $N \leq 200$
• $K \leq N$
• $T \leq 10$

Subtask 2 (7 puncte)

• $N \leq 2\ 000$
• $K \leq N$
• $T \leq 10$

Subtask 3 (5 puncte)

• $N \leq 50$
• $\sum K \leq 2\ 000$
• $T \leq 2\ 000$

Subtask 4 (6 puncte)

• $N \leq 200$
• $\sum K \leq 2\ 000$
• $T \leq 2\ 000$

Subtask 5 (7 puncte)

• $N \leq 2\ 000$
• $\sum K \leq 2\ 000$
• $T \leq 2\ 000$

Subtask 6 (8 puncte)

• $N \leq 500\ 000$
• $\sum K \leq 2\ 000$
• $T \leq 2\ 000$

Subtask 7 (9 puncte)

• $N \leq 2\ 000$

Subtask 8 (50 puncte)

• $N \leq 500\ 000$

Subtask 9 (1 punct)

• Fără restricții suplimentare

Exemplu

countbst.in

2
10 3
2 7 5
10 5
1 7 4 6 2

countbst.out

84
0

Explicații

Pentru primul test avem $84$ arbori binari de căutare cu nodurile $1, 2, ..., 10$ care conţin lanţul $(2, 7, 5)$.
Pentru al doilea test, nu există niciun arbore binar de căutare valid.