sah

Mihai a primit de ziua sa un joc de şah special. Tabla jocului are forma pătrată, de dimensiune $N$ dar unele poziţii sunt marcate ca obstacole şi ele nu pot fi ocupate cu piese. În plus, jocul său are o singură piesă, numită “nebun”. Două poziţii pe tablă sunt desemnate ca poziţie iniţială şi poziţie finală. Mihai vrea să determine o modalitate de a deplasa nebunul, cu un număr minim de mutări, astfel încât acesta să ajungă din poziţia iniţială în poziţia finală. Mihai va respecta regulile de mutare a nebunului la jocul de şah, adică din poziţia curentă nebunul se poate muta doar pe diagonală, în oricare dintre cele $4$ direcţii, oricâte poziţii deodată dar fără a sări peste obstacole. În plus, Mihai are voie la o excepţie de la această regulă: îi este permis să execute cel mult două mutări după regula de avansare a calului pe tabla de şah.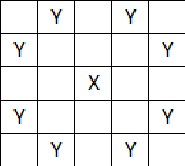

Pentru clarificare, în figura următoare, poziţia calului este marcată cu $X$. El va putea fi mutat în oricare dintre poziţiile marcate cu $Y$. La o mutare după regula calului, nu contează starea poziţiilor peste care se sare, ci doar ca poziţia finală să nu reprezinte un obstacol.

Tabla de şah are liniile numerotate de sus în jos cu numere naturale cuprinse între $1$ şi $N$ iar coloanele de la stânga la dreapta cu numere naturale cuprinse între $1$ şi $N$. O poziţie de pe tablă se identifică printr-o pereche $(i, j)$ unde $i$ reprezintă linia iar $j$ coloana acelei poziţii.

Cerinţa

Dată fiind configuraţia tablei de şah precum şi poziţiile iniţială şi finală ale piesei, se cere determinarea numărului minim de mutări pentru a deplasa piesa între cele două poziţii.

Date de intrare

Fişierul sah.in conţine pe prima linie numerele $N, i_1, j_1, i_2, j_2,$ separate prin câte un spaţiu, reprezentând: $N$ – dimensiunea tablei; $(i_1, j_1)$ – poziţia iniţială a piesei; $(i_2, j_2)$ – poziţia finală a piesei. Pe următoarele $N$ linii se găsesc câte $N$ numere din mulţimea $\{0,1\}$. Valoarea $1$ reprezintă o poziţie marcată pe tablă ca obstacol iar valoarea $0$ o poziţie liberă. Numerele de pe aceeaşi linie nu sunt separate prin spaţii.

Date de ieșire

Fişierul sah.out conţine pe prima linie un număr natural reprezentând numărul minim de mutări necesare.

Restricții și precizări

• $1 \leq N \leq 500$;
• Piesa nu poate părăsi tabla de joc;
• Se garantează că poziţia iniţială şi cea finală nu sunt marcate ca obstacole;
• Se garantează existenţa a cel puţin unei posibilităţi de mutare a piesei între poziţia iniţială şi cea finală;
• Se recomandă citirea datelor din fişier linie cu linie şi nu caracter cu caracter;

Exemplu

sah.in

4 1 1 4 1
0100
1000
0010
0000

sah.out

2

Explicație

Nebunul pleacă din $(1,1)$ foloseste săritura calului până în poziţia $(3,2)$, apoi din acea poziţie, folosind mişcarea pe diagonală sare până în poziţia finală $(4,1)$. O altă soluţie se poate obţine efectuând mutările: $(1,1) \Rightarrow (2,3)$ ; $(2,3) \Rightarrow (4,1)$