O furnică se deplasează în sistemul de coordonate xOy. Furnica pleacă din origine. Dacă furnica se găsește la coordonatele (x,y) atunci ea se va deplasa în linie dreaptă în unul din următoarele șase puncte:
(x+1, y+1)(x+2, y+2)(x+3, y+3)(x+1, y-1)(x+2, y-2)(x+3, y-3)
Furnica se va deplasa astfel încât în niciun moment al deplasării să nu se găsească într-un punct de coordonată y negativă. La final furnica va ajunge pe axa Ox.
Cerință
Cunoscând numărul de deplasări de fiecare din cele șase tipuri să se aleagă o ordine în care acestea pot fi efectuate astfel încât suprafața delimitată inferior de axa Ox și superior de traseul furnicii să aibă aria minimă.
Date de intrare
Fișierul de intrare minarea.in va conține 6 numere naturale a, b, c, d, e, f separate prin câte un spațiu, reprezentând numărul de deplasări de tip 1, 2, 3, 4, 5 respectiv 6.
Date de ieşire
Fișierul de ieșire minarea.out va conține un singur număr reprezentând aria minimă.
Restricţii și precizări
0 ≤ a, b, c, d, e, f ≤ 2 000 000 000a + 2b + 3c = d + 2e + 3f- pentru teste în valoare de
10punctec=f=0
Exemplu
minarea.in
2 0 1 1 2 0
minarea.out
13
Explicații
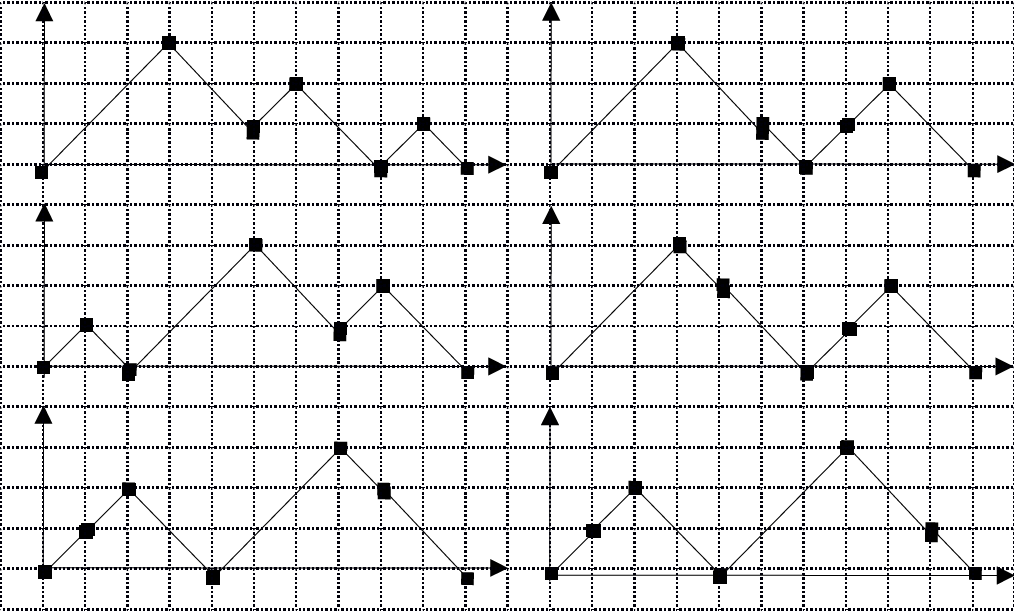
Aria minimă este 13. Această arie poate fi obținută în mai multe moduri. În figura de mai jos sunt descrise toate cele șase moduri în care traseul furnicii și axa Ox ar putea delimita o suprafața de arie 13.
minarea.in
219 221 5 108 47 158
minarea.out
1760
Explicații
Aria minimă este 1760.