Şoricelul Jerry este (pentru a câta oară ?) în labirint. Labirintul poate fi codificat ca o matrice cu linii şi coloane fomată din celule pătratice identice. Liniile se numerotează de la la , iar coloanele de la la . Labirintul este format din celule libere şi din celule ocupate de pereţii labirintului.
La momentul iniţial, Jerry se găseşte într-o anumită celulă liberă şi misiunea lui este să ajungă la destinaţie într-o altă celulă liberă precizată. Șoricelul se poate deplasa din celula curentă în oricare dintre cele patru celule cu care aceasta are în comun o latură şi nu poate ieşi în afara labirintului. Este posibil ca el să nu poată să ajungă de la poziţia iniţială la cea finală trecând doar prin celule libere. În această situație el este nevoit să sfarme peretele în anumite celule. Jerry şi-a pregătit dinamită în acest scop, pentru că nu i se pare optim să roadă peretele cu dinţii.
Cerinţă
Cunoscând dimensiunile şi ale labirintului, coordonatele celulei de plecare şi ale celulei destinaţie, precum şi coordonatele celulelor ocupate de pereţi, să se determine numărul minim de celule ocupate, pe care Jerry trebuie să le dinamiteze pentru a putea să ajungă la destinaţie.
Date de intrare
Fişierul de intrare labir.in conţine pe prima linie două numere naturale şi separate printr-un spaţiu, reprezentând numărul de linii, respectiv numărul de coloane ale matricei care codifică labirintul. Pe linia a doua se găsesc patru numere naturale , , , separate prin câte un spaţiu, reprezentând poziţia de plecare, respectiv poziţia destinaţie. Pe linia a treia se găseşte un număr natural , reprezentând numărul de celule ocupate. Pe fiecare dintre următoarele linii se vor găsi câte două numere şi separate printr-un spaţiu, reprezentând linia şi coloana unei celule ocupate.
Date de ieșire
Pe prima linie a fişierului labir.out se va scrie un singur număr natural , reprezentând numărul minim de celule pe care Jerry trebuie să le dinamiteze pentru a ajunge la destinaţie.
Restricții și precizări
- Se garantează că pentru toate testele există cel puţin linii şi/sau coloane formate numai din celule neocupate.
- Pentru dintre teste
Exemplu
labir.in
7 8
1 1 7 8
6
2 1
1 2
3 1
6 7
6 8
6 2
labir.out
1
Explicație
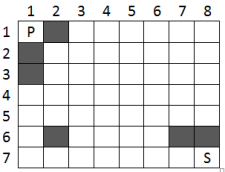
Celulele ocupate au fost colorate în gri. Șoricelul pleacă din celula notată cu și sosește în celula . Pentru aceasta el dinamitează celula și ajunge în dinamitând un număr minim , de celule ocupate.