Ninel, fratele mai mic al lui Gigel, a primit de ziua lui un joc tetris în care toate piesele sunt formate din maxim 3 pătrățele. Există 4 tipuri de astfel de piese care, luând în considerare rotirile pieselor, se pot plasa pe un grid în 9 moduri distincte:



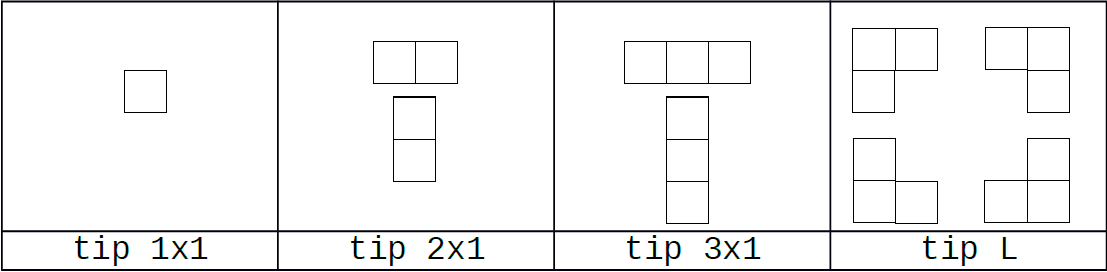
Jocul conține din fiecare tip de piesă cel puțin 2 și cel mult 100 de bucăți. El dorește să plaseze toate piesele astfel încât acestea să formeze un ciclu, adică orice pătrățel să aibă exact doi vecini pe cele patru direcții (sus, jos, dreapta, stânga) și zona interioară ciclului să fie conexă pe cele patru direcții.

O mulțime de pătrățele se consideră zonă conexă dacă din oricare pătrățel din mulțime se poate ajunge în oricare alt pătrățel trecând doar prin pătrățele din mulțime pe cele patru direcții.

Cerință

Cunoscând numărul de piese din fiecare tip, ajutați-l pe Ninel să rezolve problema.

Date de intrare

Fișierul tris.in conține pe o singură linie 4 numere naturale a b c d, separate prin câte un spațiu, reprezentând numărul de piese de tipul 1x1, 2x1, 3x1 respectiv L în această ordine.

Date de ieșire

Fișierul tris.out va conține pe prima linie două numere n și m, reprezentând dimensiunile matricii-soluție.
Pe următoarele n linii se vor afla câte m numere naturale din mulțimea {0, 1, … , a+b+c+d }, fiecare element semnificând:

• 0 – dacă pe poziția respectivă nu se găsește niciun element;
• i – dacă pe poziția respectivă este plasată una din cele a+b+c+d piese, identificată cu numărul i.
  Piesele pot fi numerotate în orice ordine cu numere de la 1 la a+b+c+d, cu condiția ca acestea să aibă numere distincte.

Evaluare

O soluție se consideră validă dacă și numai dacă se respectă următoarele condiții:

• dimensiunile matricei sunt cel mult egale cu 800x800;
• fiecare celulă ocupată de o piesă are exact 2 vecini;
• zona ocupată de piese formează un ciclu;
• zona interioară ciclului este conexă pe cele patru direcții.

Restricții și precizări

• pentru datele de intrare problema întotdeauna are soluție;
• pentru 32 de puncte 10 ≤ a, b, c, d ≤ 100;
• pentru 52 de puncte 5 ≤ a, b, c, d ≤ 100;
• pentru 72 de puncte 3 ≤ a, b, c, d ≤ 100;
• pentru 100 de puncte 2 ≤ a, b, c, d ≤ 100;
• au fost adăugate teste și a fost schimbată împărțirea punctelor

Exemplu

tris.in

3 4 3 4 

tris.out

11 6
0 1 2 4 4 4
1 1 0 0 0 3
8 0 0 0 3 3
8 0 0 0 9 0
8 0 0 0 9 9
10 0 0 0 0 13
10 0 0 0 0 11
12 0 0 0 0 11
12 0 0 0 0 14
6 0 0 0 0 7
6 5 5 5 7 7

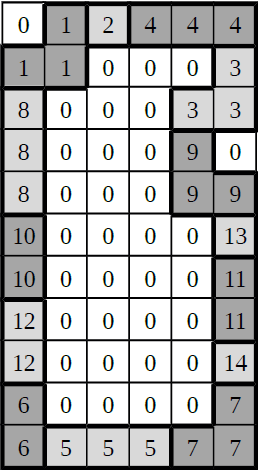
Avem 3 piese de tip 1x1
Avem 4 piese de tip 2x1
Avem 3 piese de tip 3x1
Avem 4 piese de tip L
Matricea-soluție este formată din 11 linii și 6 coloane

Observație:

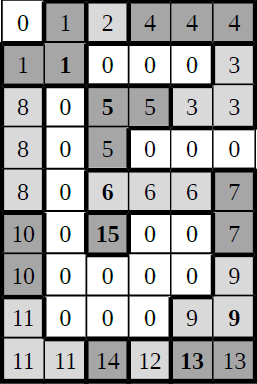
Următorea matrice nu formează soluție din multiple motive:

• există pătrățele care nu au exact doi vecini (vezi piesele 6, 9, 13 și respectiv 15);
• zona interioară ciclului nu este conexă pe cele patru direcții. Există două zone interioare conexe cu 3 pătrățele, respectiv 13 pătrățele.