Bob Ross

Bob Ross este foarte faimos pentru picturile sale în ulei cu peisaje muntoase. Astăzi s-a hotărât să picteze o nouă operă, dar va aborda procesul său de creație într-un mod inedit.

Bob dispune de $N$ puncte pe o pânză infinită, al $i$-lea punct având coordonatele ($x_i, y_i$). Punctele au proprietatea că $x_i$ < $x_{i+1}$. El își va alege un număr de puncte și pentru fiecare punct ales $i$, va colora segmentele dintre perechile de puncte ($i - 1, i$) și ($i, i+1$).

Alegând o submulțime a celor $N$ puncte, el va colora segmentele incidente acestor puncte în următorul mod: de fiecare dată când își alege un punct, va colora segmentele incidente cu acel punct (orice punct are doi vecini, cu excepția primului și ultimului punct, care au doar un vecin). Dacă un segment este deja colorat, atunci nu va fi colorat a doua oară, și nici cantitatea de vopsea de pe pensulă nu va scădea.

Inițial, Bob are o pensulă cu o cantitate $V$ de vopsea. Cantitatea de vopsea necesară pentru a colora un segment este egală cu pătratul lungimii acelui segment, iar după colorare cantitatea de vopsea de pe pensulă scade cu această valoare.

Cerința

Bob s-a gândit la următoarele $K$ scenarii. Dacă la scenariul $i$ ar avea o pensulă cu o cantitate $V_i$ de vopsea, care este numărul maxim $P_i$, astfel încât oricum am alege $P_i$ puncte, să poată colora toate segmentele adiacente acelor puncte?

Date de intrare

Prima linie din fișierul de intrare ross.in va conține un singur număr $N$ reprezentând numărul de puncte de pe pânza lui Bob. Pe următoarele $N$ linii se vor afla câte $2$ numere $x_i$, $y_i$ separate printr-un spațiu, reprezentând coordonatele punctului $i$. Pe următoarea linie se află numărul $K$ de scenarii ale lui Bob. Pe următoarele $K$ linii se va afla câte un număr $V_i$ reprezentând cantitatea de vopsea de pe pensulă pentru scenariul $i$.

Date de ieșire

Fișierul de ieșire ross.out va conține $K$ linii, linia $i$ având un singur număr $P_i$ reprezentând răspunsul pentru scenariul $i$.

Restricții și precizări

• $1 \leq N \leq 2 \ 000$
• $1 \leq K \leq 10^5$
• $1 \leq x_i, y_i \leq 10^6$
• $0 \leq V_i \leq 10^{15}$
• $x_i < x_{i + 1}$; $\forall i \in \{1, 2, \dots, N - 1 \}$;
• Pentru teste in valoare de $17$ puncte: $N \leq 15$, $K \leq 10$
• Pentru alte teste in valoare de $13$ puncte: $N \leq 20, K \leq 10^5$
• Pentru alte teste in valoare de $11$ puncte: $N, K, V_i, x_i, y_i \leq 100$
• Pentru alte teste in valoare de $24$ de puncte: $N \leq 200$
• Pentru alte teste in valoare de $35$ de puncte: Nu există restricții suplimentare.

Exemplul 1

ross.in

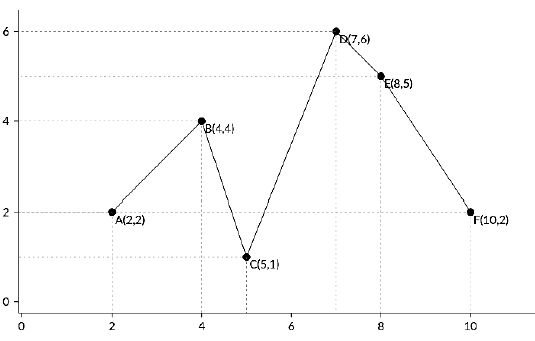
6
2 2
4 4
5 1
7 6
8 5
10 2
2
44
55

ross.out

1
2

Explicație

Pentru $V = 44$ răspunsul este $1$. Oricum am alege un punct, putem colora segmentele adiacente acestuia. Există totuși perechi de $2$ puncte, care pentru colorare, necesită o cantitate de vopsea mai mare decât $44$ (spre exemplu, alegând punctele ($5, 1$) și ($10, 2$), avem nevoie de o pensulă cu o cantitate de vopsea mai mare sau egală ca $52$).

Pentru $V = 55$ răpsunsul este $2$. Pentru oricare $2$ perechi de puncte alese, cantitatea de de vopsea necesară este mai mică sau egală cu $55$. Alegând punctele ($4, 4$), ($7, 6$) și ($10, 2$), costul colorării depașește $55$, deci răspunsul este $2$.