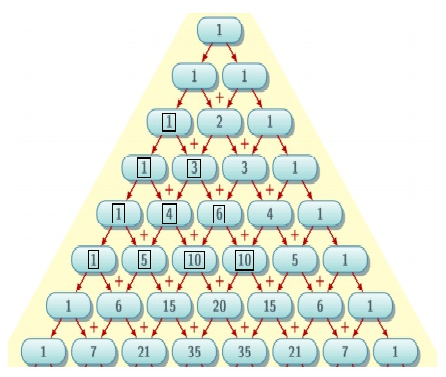
Se consideră aranjamentul piramidal de numere din figură (cunoscut și sub denumirea de triunghiul lui Pascal). În vârful și pe marginile laterale ale piramidei se află numărul . Restul numerelor din acest triunghi se formează ca suma celor două numere de deasupra. Definim un ca fiind un triunghi echilateral de numere din interiorul triunghiului lui Pascal, pentru care se precizează poziția a vârfului și , lungimea laturii. ( = rând, = coloană, = lungime latură).
- reprezintă triunghiul de numere cu vârful poziționat pe rândul al treilea, primul element și care are lungimea laturii de elemente, adică numerele (), (, ), (, , ), (, , , ) – scrise de sus în jos și de la stânga la dreapta. Pe figura de mai sus, are elementele încadrate în dreptunghiuri.
Notăm cu suma elementelor unui .
Cerinţă
Să se scrie un program care determină numărul , cunoscând numerele , și ce definesc un . Pentru că poate fi foarte mare, se va calcula modulo .
Date de intrare
Fişierul de intrare tripas.in conţine pe primul rând numerele naturale , și separate prin câte un spațiu.
Date de ieșire
Fişierul de ieşire tripas.out va conţine pe prima linie restul împărțirii numărului la .
Restricții și precizări
Exemplu
tripas.in
3 1 4
tripas.out
42
Explicație
Triunghiul cu vârful situat pe primul element de pe rândul al treilea și cu lungimea laturii de elemente, are suma elementelor + + + + + + + + + = .