cerc

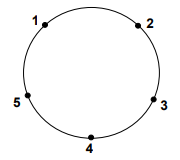
$N$ puncte numerotate de la $1$ la $N$ sunt aşezate pe cerc, în sensul acelor de ceasornic, în ordine strict crescătoare. Există $M$ segmente de dreaptă diferite care unesc $M$ perechi de puncte dintre cele $N$ date. Cele două puncte care formează orice pereche sunt distincte. Distanţele dintre două puncte succesive sunt alese astfel încât să nu existe $3$ sau mai multe segmente care trec printr-un acelaşi punct interior cercului.

Cerinţă

Cunoscându-se numărul de puncte, numărul de perechi şi perechile de puncte care vor fi unite, se cere să se determine numărul $P$ de puncte de intersecţie formate de acestea în interiorul cercului (punctele de intersecţie aflate chiar pe cerc nefiind luate în considerare).

Date de intrare

Fişierul de intrare cerc.in conţine:

• pe prima linie două numere $N$ şi $M$ despărţite printr-un spaţiu, numere reprezentând numărul de puncte şi respectiv numărul de segmente;
• pe următoarele $M$ linii, câte o pereche de numere dinstincte $p_{i_1}$, $p_{i_2}$ despărţite prin câte un spaţiu, numere reprezentând capetele câte unui segment.

Date de ieșire

Fişierul de ieşire cerc.out va conţine un singur număr $P$ reprezentând numărul total de puncte de intersecţie formate în interiorul cercului. Dacă acest număr depăşeşte $999 \ 999$, atunci se va scrie numărul format numai din ultimele sale $6$ cifre.

Restricții și precizări

• $1 \leq N \leq 500$, număr natural
• $0 \leq M < 125 \ 000$, număr natural
• $1 \leq p_{i_1} < p_{i_2} \leq N$, numere naturale, oricare $i \in \{1, \dots, M \}$
• Nu există două perechi $p_{i_1}$, $p_{i_2}$ identice

Exemplu

cerc.in

5 6
1 2
1 3
1 4
2 4
3 5
4 5

cerc.out

3

Explicație

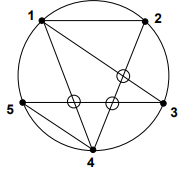
S-au format în interiorul cercului $3$ puncte de intersecţie (marcate prin cerculeţe pe figura alăturată).