Considerăm un caroiaj dreptunghiular cu linii şi coloane. Liniile sunt numerotate de la la de sus în jos şi coloanele de la la , de la stânga la dreapta. Caroiajul este împărţit în x pătrate cu latura egală cu două unităţi . În fiecare pătrat al caroiajului se găseşte una dintre valorile sau . Se cunoaşte o poziţie a unuia dintre pătratele caroiajului (, ). Trebuie construit un cerc care să îndeplinească următoarele proprietăţi:
- Centrul cercului să coincidă cu centrul pătratului din poziţia ;
- Raza cercului să fie un număr natural nenul;
- Diferenţa dintre numărul de valori şi numărul de valori aflate în pătratele acoperite de cerc să fie maximă.
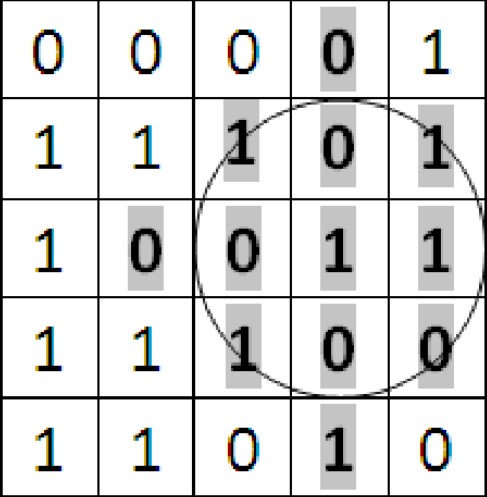
Considerăm că un pătrat este acoperit de cerc dacă pătratul şi cercul au cel puţin un punct comun (aflat pe contur sau în interior). Dacă un pătrat este complet inclus în interiorul cercului se consideră că şi acel pătrat este acoperit de cerc (în figură, cercul desenat “acoperă” inclusiv pătratul din poziţia ). Cercul din figură are raza .
Cerinţă
Determinaţi diferenţa maximă ce se poate obţine cu constrângerile de mai sus.
Date de intrare
Fişierul cerc.in conţine pe prima linie patru numere naturale şi separate prin câte un spaţiu, cu semnificaţia din enunţ. Pe următoarele linii se găsesc câte numere naturale din mulţimea , care reprezintă valorile din pătratele caroiajului. Numerele de pe aceste linii nu sunt separate prin spaţii.
Date de ieșire
Fişierul cerc.out conţine pe prima linie un singur număr întreg reprezentând valoarea maximă a diferenţei cerute.
Restricții și precizări
- Se recomandă citirea matricei din fişier linie cu linie şi nu element cu element;
- Cercul poate avea raza astfel încât să ocupe zone şi în afara caroiajului, dar acele zone nu influenţează valoarea căutată;
Exemplu
cerc.in
5 5 3 4
00000
00101
01110
00110
10010
cerc.out
4
Explicație
Valoarea maximă, se poate obţine pentru un cerc de rază .