Fie un șir de coloane de ciment (pozițiile lor fiind numerotate de la la ) de aceeași lățime și diverse înălțimi. Ele sunt încadrate la stânga (poziția ) și la dreapta (poziția ) de ziduri foarte înalte. Apa începe să curgă de deasupra primei coloane, câte o pătrățică de apă pe secundă. Apa se acumulează dacă are pereți în stânga și în dreapta, altfel curge mai jos către dreapta. Deasupra fiecărei coloane de ciment se poate forma astfel o coloană de apă, cu înălțimea egală cu numărul de pătrățele de la nivelul apei până la zona de contact cu coloana de ciment.
Cerință
- Care este înălțimea a celei mai înalte coloane de apă după ce apa a ajuns peste tot la înălțimea celei mai înalte coloane de ciment?
- Care este numărul de secunde în care apa ajunge să acopere coloana numărul ?
- Care este poziția a celei mai din dreapta coloane acoperită de apă după secunde?
- Care este poziția a celei mai din stânga coloane pe care o putem reduce cu o unitate astfel încât apa să ajungă cât mai repede la coloana ?
Date de intrare
Fișierul de intrare inundatie.in conține pe prima linie un număr natural , reprezentând cerința ce trebuie rezolvată(, sau ). Pe a doua linie numerele și despărțite prin câte un spațiu cu semnificația din enunț. Pe a treia linie se găsesc numere naturale separate prin câte un spațiu ce reprezintă înălțimile coloanelor.
Date de ieșire
Fișierul de ieșire inundatie.out va conține un singur număr, astfel:
Dacă : înălțimea cu semnificația de mai sus.
Dacă : timpul cu semnificația de mai sus.
Dacă : poziția cu semnificația de mai sus.
Dacă : poziția cu semnificația de mai sus.
Restricții și precizări
- înălțimea oricărei coloane din șir
- ;
- O coloană de înălțime este acoperită de apă dacă apa a ajuns la înălțimea .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 11 | |
| 2 | 25 | |
| 3 | 33 | |
| 4 | 31 |
Exemplul 1
inundatie.in
1
32 15 45
8 5 5 4 3 3 7 5 4 3 3 5 4 3 4 5 6 5 4 4 3 4 5 4 3 2 1 2 3 4 5 9
inundatie.out
8
Exemplul 2
inundatie.in
2
32 15 45
8 5 5 4 3 3 7 5 4 3 3 5 4 3 4 5 6 5 4 4 3 4 5 4 3 2 1 2 3 4 5 9
inundatie.out
21
Exemplul 3
inundatie.in
3
32 15 45
8 5 5 4 3 3 7 5 4 3 3 5 4 3 4 5 6 5 4 4 3 4 5 4 3 2 1 2 3 4 5 9
inundatie.out
29
Exemplul 4
inundatie.in
4
32 15 45
8 5 5 4 3 3 7 5 4 3 3 5 4 3 4 5 6 5 4 4 3 4 5 4 3 2 1 2 3 4 5 9
inundatie.out
7
Explicații
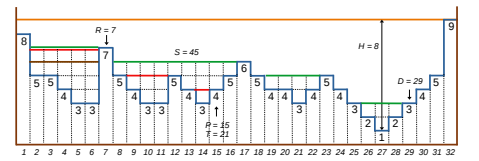
Toate exemplele se referă la figura de mai sus, diferă doar numărul cerinței. În toate și .
Primul exemplu: Linia portocalie de înălțime este nivelul apei la momentul când toate coloanele devin acoperite de apă.
Cea mai înaltă coloană de apă este cea cu numărul , având pătrățele de apă.
Al doilea exemplu: În imaginea de mai sus, liniile roșii arată nivelurile apei la momentul când apa acoperă coloana de la poziția . Observăm că sunt de pătrățele de apă sub linie, deci este nevoie de de secunde pentru a acoperi coloana .
Al treilea exemplu: Linia verde arată nivelul apei după de secunde. Ea acoperă coloana numărul . Lăsând apa să curgă încă secunde (până la cele secunde) nivelul nu se ridică suficient pentru a ajunge la coloana deoarece ar mai fi nevoie de pătrățele de apă, adică încă secunde.
Al patrulea exemplu: Cea mai din stânga coloană pe care o vom reduce cu unu este coloana numărul . Astfel apa va ajunge cu secunde mai devreme la coloana . Linia maro (linia de apă de înălțime care se întinde de la coloana la coloana ) arată cele pătrățele cu care reducem timpul. Orice altă coloană am reduce nu va ajunge așa repede.