optime

Maria iubește numerele prime. Ea scrie pe o foaie de hârtie, în ordine strict crescătoare, un șir format din numerele prime care au cel puțin $2$ cifre. Apoi, din numerele care conțin mai mult de $2$ cifre taie cifrele din stânga, astfel încât să rămână exact $2$ cifre. Dacă după tăierea cifrelor numărul obținut nu este cuprins între $10$ și $99$, numărul este eliminat din șir. De exemplu, numărul prim $101$, care are $3$ cifre, nu va fi scris, deoarece i se taie cifra din stânga, rezultând numărul $01$, adică $1$, care nu are exact $2$ cifre, deci după tăiere va fi eliminat din șir.

Maria umple un tabel cu $2 \cdot k$ linii și $k$ coloane, astfel încât, parcurgându-l pe linii, de sus în jos și fiecare linie de la stânga la dreapta, se obțin numerele din șir. Studiind numerele din tabel, constată că printre acestea se află și numere care nu sunt prime.

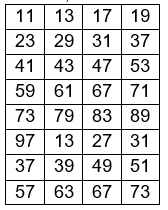
De exemplu, pentru $k=4$, tabelul arată ca în imaginea din dreapta.

Cerință

Cunoscând un număr natural $k$ nenul și un număr natural $x$, ajutați-o pe Maria:

1. Să determine suma numerelor din tabel care nu sunt prime. Dacă nu există numere care nu sunt prime, suma are valoarea $0$.
2. Să aleagă $x$ coloane consecutive din tabel, astfel încât acestea să conțină, în total, un număr maxim de numere prime. Dacă există mai multe posibilități, se va alege secvența de coloane consecutive care are o valoare cât mai mare a coloanei de început din secvență. Să se determine numărul primei coloane din secvența aleasă, precum și numărul total de numere prime din secvență.

Date de intrare

Fişierul de intrare optime.in conţine pe prima linie o cifră $C$ care poate să fie doar $1$ sau $2$. Dacă $C = 1$, pe linia a doua se găsește un număr natural nenul $k$ cu semnificația din enunț. Dacă $C = 2$, pe linia a doua se află două numere naturale nenule, $k$ și $x$, cu semnificația din enunț.

Date de ieșire

Dacă valoarea lui $C$ este $1$, atunci se va rezolva numai punctul $1$ din cerință. În acest caz, fişierul de ieşire optime.out va conţine pe prima linie un număr natural reprezentând valoarea sumei determinate.

Dacă valoarea lui $C$ este $2$, se va rezolva numai punctul $2$ din cerință. În acest caz, fişierul de ieşire optime.out va conţine pe prima linie un număr natural reprezentând numărul de ordine al primei coloane conform cerinței, iar pe linia a doua numărul de numere prime, conform cerinței.

Restricții și precizări

• $1 \leq x \leq k \leq 200$;
• Pentru rezolvarea primei cerinţe se acordă $30\%$ din punctaj, iar pentru cerința a doua se acordă $70\%$ din punctaj.

Exemplul 1

optime.in

1
4

optime.out

286

Explicație

Pentru $k = 4$, în tabel se află următoarele numere neprime: $27$, $39$, $49$, $51$, $57$, $63$, suma lor fiind $286$.

Exemplul 2

optime.in

2
4 3

optime.out

2
19

Explicație

Coloana $1$ conține $7$ numere prime, coloana $2$ conține $6$ numere prime, coloana $3$ conține $6$ numere prime, iar coloana $4$ conține $7$ numere prime.

Putem alege fie coloanele $1,2,3$, fie coloanele $2,3,4$, ambele variante conținând câte $19$ numere prime. Se alege a doua variantă, pentru că are valoarea mai mare a coloanei de început a secvenței.