pietre

O tablă de joc cu $n$ linii, numerotate de la $1$ la $n$ și $m$ coloane, numerotate de la $1$ la $m$ conține $n * m$ celule identice. Celula din colţul din stânga sus se află pe linia $1$ şi coloana $1$. O celulă poate fi: celulă liberă, celulă în care se află o piatră sau celulă de tip gaură.

Pietrele sunt numerotate cu valori începând de la $1$. Numerotarea pietrelor pe tablă se face în ordinea în care sunt date în fișierul de intrare.

O celulă de pe tablă are maxim patru celule vecine, aflate în direcțiile: nord, vest, sud, est, iar o piatră poate sări doar
peste o celulă vecină în care se află o piatră. În urma unei astfel de sărituri, piatra peste care s-a sărit dispare de pe tablă. Astfel, o piatră situată în celula de pe linia $i$ şi coloana $j$, poate sări :

• în direcția nord peste piatra situată în celula de pe linia $i-1$ și coloana $j$ și ajunge în celula de pe linia $i-2$ și coloana $j$, iar piatra aflată pe linia $i-1$ și coloana $j$ dispare; o astfel de săritură se notează cu litera N;
• în direcția est peste piatra situată în celula de pe linia $i$ și coloana $j+1$ și ajunge în celula de pe linia i și coloana $j+2$, iar piatra aflată pe linia $i$ și coloana $j+2$ dispare; o astfel de săritură se notează cu litera E;
• în direcția sud peste piatra situată în celula de pe linia $i+1$ și coloana j și ajunge în celula de pe linia i+2 și coloana $j$, iar piatra aflată pe linia $i+1$ și coloana $j$ dispare; o astfel de săritură se notează cu litera S;
• în direcția vest peste piatra situată în celula de pe linia $i$ și coloana $j-1$ și ajunge în celula de pe linia i și coloana $j-2$, iar piatra aflată pe linia $i$ și coloana $j-1$ dispare; o astfel de săritură se notează cu litera V. O săritură a unei pietre este permisă doar dacă celula în care urmează să ajungă se află pe tabla de joc, este liberă și în celula peste care sare există o piatră.

Se cunoaște o succesiune de sărituri formată din maxim $255$ de caractere S, N, E sau V, după care o piatră realizează săriturile specificate, în ordine, de la stânga la dreapta. Dacă piatra ar trebui execute o săritură care nu este permisă, poziţia ei nu se modifică şi se trece la săritura următoare din succesiune.

Cerință

Să se determine numărul pietrei care efectuând sărituri în conformitate cu succesiunea dată, conduce la o configuraţie finală formată dintr-un număr minim de pietre pe tablă. Dacă există mai multe pietre care ar conduce la acelaşi număr minim de pietre în configuraţia finală, se va afişa valoarea cea mai mică dintre numerele de identificare ale pietrelor respective.

Date de intrare

Fişierul de intrare pietre.in va conţine:

• pe prima linie din fişier numărul natural $n$ care reprezintă numărul de linii, numărul natural $m$ care reprezintă numărul de coloane, numărul natural de pietre $k$ şi numărul natural de găuri $g$, valori separate între ele două câte două printr-un spaţiu;
• pe următoarele $k$ linii, câte două valori separate două câte două printr-un spaţiu, reprezentând linia şi coloana unei pietre;
• pe următoarele $g$ linii, câte două valori separate două câte două printr-un spaţiu, reprezentând linia şi coloana unei găuri;
• pe ultima linie se află succesiunea de sărituri.

Date de ieșire

Fişierul de ieşire pietre.out va conţine:

• pe prima linie numărul pietrei căreia aplicându-i-se succesiunea de sărituri conduce la configuraţia conţinând cel mai mic număr de pietre;
• pe a doua linie se află numărul de pietre din configuraţia finală (fie acesta $t$) ;
• pe următoarele $t$ linii se află câte două valori, separate între ele printr-un spaţiu, reprezentând linia şi coloana fiecărei pietre rămase pe tablă, începând cu cea mai de sus (linia cea mai mică) şi coloana cea mai din stânga (coloana cea mai mică) şi până la piatra cea mai de jos cu linia cea mai de jos (cea mai mare) şi coloana cea mai din dreapta (cea mai mare).

Restricții și precizări

• $2 \leq n, m \leq 100$
• $2 \leq k \leq n \cdot m - 1$
• $0 \leq g \leq n \cdot m - 1$
• Se garantează că în fiecare test există cel puţin o piatră care efectuează cel puţin o săritură.

Exemplul 1

pietre.in

5 4 6 2
1 1
1 2
2 2
3 2
3 3
4 1
3 4
5 3
VSE

pietre.out

5
4
1 1
1 2
2 2
5 1

Explicație

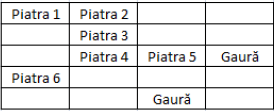
Configurația inițială este în figura alăturată.

Piatra $1$: nu poate efectua săritura V (deoarece ar părăsi tabla de joc), nici săritura S (pentru că nu există nicio piatră în celula vecină aflată în direcția sud), efectuează săritura E, deci configurația finală a tabelei va conține $5$ pietre.

Pentru piatra $2$ se obține configurația finală identică celei inițiale, deoarece nu poate efectua nicio săritură.

Piatra $3$ poate efectua doar săritura S. Configurația finală conține $5$ pietre.

Piatra $4$ nu poate efectua nicio săritură. Configurația finală conține $6$ pietre.

Piatra $5$ poate efectua săriturile: V și dispare piatra $4$, S și dispare piatra şi nu poate efectua săritura E. Configurația finală are $4$ pietre și este în figura alăturată.

Piatra $6$ nu poate efectua nicio săritură. Configurația finală conține $6$ pietre.