roșii mici

Dan este un mare pasionat al fructelor, printre preferatele sale fiind strugurii şi pepenii. Însă recent şi-a descoperit şi pasiunea pentru legume, în special pentru roşii, dar mai ales roşiile mici. Spre norocul lui, grădina bunicului este plină de roşii.
Grădina are forma unei matrice cu $N$ linii şi $M$ coloane cu elemente numere naturale, nu neapărat distincte, unde fiecare element din matrice reprezintă dimensiunea unei roşii. Matricea are proprietatea că oricare coloană are valorile ordonate crescător de sus în jos, adică de la prima spre ultima linie. Bunicul său îi cere să rezolve $Q$ sarcini. Pentru fiecare sarcină, Dan primeşte un număr natural $x$ şi trebuie să găsească o submatrice de arie maximă care începe de pe linia $1$ a matricei care reprezintă grădina şi are toate elementele mai mici sau egale decât $x$. Pentru determinarea submatricei cerute, Dan are voie să mute toate valorile unei coloane în faţa oricărei alte coloane. De asemenea, îi este permis să facă oricâte mutări de tipul acesta.

Cerință

Să se calculeze aria maximă a unei submatrice care respectă specificaţiile din enunţ, pentru fiecare din cele Q sarcini date de către bunic.

Date de intrare

Fişierul rosiimici.in conţine pe prima linie trei numere naturale $N$, $M$ şi $Q$ separate printr-un spaţiu, având semnificaţia din enunţ.
Pe fiecare dintre următoarele $N$ linii se află câte $M$ numere naturale despărţite prin câte un spaţiu, reprezentând valorile matricei.
Pe următoarele $Q$ linii se află câte un număr natural $x$, reprezentând dimensiunea unei roşii.

Date de ieșire

Fişierul rosiimici.out va conţine pe primele $Q$ linii câte un număr natural, reprezentând aria maximă cerută pentru fiecare sarcină, în ordinea în care acestea apar în fişierul de intrare.

Restricții și precizări

• $1 \leq N, M ≤ 1 \ 000$
• $1 \leq Q ≤ 100 \ 000$
• $1 \leq A[i][j] \leq N \cdot M, 1 \leq i \leq N, 1 \leq j \leq M$
• $1 \leq x \leq N \cdot M$

Exemplul

rosiimici.in

3 4 3
1 9 6 2
1 10 10 4
7 15 10 6
6
10
9

rosiimici.out

4
9
6

Explicație

Pentru rezolvarea primei sarcini Dan mută prima coloană în faţa celei de a patra obţinând matricea:
Alege apoi submatricea cu colţul stânga sus în $(1,3)$ şi colţul dreapta jos în $(2, 4)$. Aria acesteia este $4$.

Pentru rezolvarea celei de a doua sarcini, Dan mută prima coloană în faţa celei de a treia obţinând matricea:
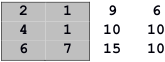Soluţia este submatricea cu colţul stânga sus în $(1,2)$ şi colţul dreapta jos în $(3, 4)$. Aria acesteia este $9$.

Pentru rezolvarea celei de a treia sarcini, Dan mută ultima coloană în faţa primei coloane, obţinând matricea:
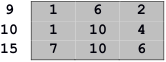Soluţia este submatricea cu colţul stânga sus în $(1,1)$ şi colţul dreapta jos în $(3, 2)$. Aria acesteia este $6$.