Z

Magazinul de jocuri a lansat cea mai recentă versiune a jocului Z, pentru a-i ajuta pe elevii din clasa a $VIII$-a să înțeleagă mai bine modul de identificare a coordonatelor unui punct din plan, într-un sistem de axe ortogonale.

Numim semn Z în planul xOy figura obținută cu ajutorul a $4$ puncte distincte $A(x_A, y_A), B(x_B, y_B), C(x_C, y_C), D(x_D, y_D),$ unite ca în fig.1, în care $x_A = x_C , x_B = x_D , y_A = y_B , y_C = y_D$.

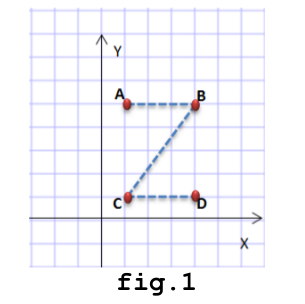
Pe ecran este afișată o foaie de matematică și sistemul de axe ortogonale $xOy$. Succesiv, apar coordonatele întregi ale unor puncte din plan. Jucătorul trebuie să marcheze pe foaie fiecare punct și să traseze un segment care să unească punctul (cu excepția primului punct marcat) cu cel marcat anterior.

În exemplul din fig.2 au fost marcate succesiv punctele: $(-8,4)$, $(-5,6)$, $(-2,6)$, $(1,6)$, $(-2,2)$, $(-5,-2)$, $(-5,2)$, $(1,2)$, $(-5,-2)$, $(1,-2)$, $(-1,2)$, $(2,6)$, $(-1,2)$, $(1,-2)$. Se observă că punctele se pot repeta.

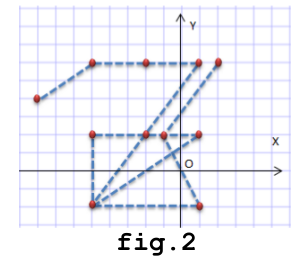
La sfârșitul jocului, jucătorul trebuie să numere de câte ori a trecut prin originea sistemului de coordonate $O(0,0)$ și care este numărul maxim al semnelor $Z$ distincte, formate cu puncte marcate.

Cerință

Cunoscându-se $N$ (numărul de puncte afișate succesiv pe ecran) și coordonatele celor $N$ puncte din plan, să se scrie un program care determină:

1. Numărul de treceri prin originea sistemului de coordonate.
2. Numărul maxim al semnelor $Z$ distincte, formate cu puncte marcate.

Date de intrare

Fișierul de intrare z.in conține pe prima linie un număr natural $P$ reprezentând cerinţa care trebuie să fie rezolvată ($1$ sau $2$). Pe cea de a doua linie se află numărul natural $N$, reprezentând numărul punctelor afișate succesiv pe ecran. Pe următoarele $N$ linii se află câte două numere întregi, $x$ și $y$, separate printr-un spațiu, reprezentând coordonatele unui punct (x,y) din plan, în ordinea apariției pe ecran.

Date de ieșire

Dacă cerinţa este $P=1$, atunci pe prima linie a fişierului z.out va fi scris un număr natural reprezentând numărul de treceri prin originea sistemului de coordonate.

Dacă cerinţa este $P=2$, atunci fişierul de ieşire z.out va conţine numărul maxim al semnelor $Z$ distincte, formate cu puncte marcate.

Restricții și precizări

• $4 \leq N \leq 1 \ 000$
• $-1 \ 000 \leq x, y \leq 1 \ 000$
• $0$ trecere prin originea sistemului de coordonate este determinată de trasarea unui segment care conține originea sistemului și are capetele diferite de origine.
• Pentru rezolvarea corectă a primei cerinţe se va acorda $20\%$ din punctaj, iar pentru rezolvarea corectă a celei de a doua cerințe se va acorda $80\%$ din punctaj.

Exemplul 1

z.in

1
14
-8 4
-5 6
-2 6
1 6
-2 2
-5 -2
-5 2
1 2
-5 -2
1 -2
-1 2
2 6
-1 2
1 -2

z.out

2

Explicație

A trecut de două ori prin originea sistemului de coordonate.

Exemplul 2

z.in

2
14
-8 4
-5 6
-2 6
1 6
-2 2
-5 -2
-5 2
1 2
-5 -2
1 -2
-1 2
2 6
-1 2
1 -2

z.out

3

Explicație

S-au format $3$ semne $Z$, reprezentate în figurile $3$, $4$ și $5$.