cristale

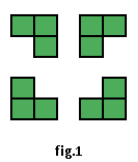
Pietrele preţioase au fascinat omenirea încă din timpuri străvechi iar cele mai renumite dintre ele, cristalele, au devenit atât simbolul durităţii cât şi al eternităţii. În urma unui studiu ştiinţific, pe un eşantion de formă dreptunghiulară se pot observa diferite tipuri de molecule, dispuse într-o geometrie perfectă, pe $M$ rânduri a câte $N$ molecule fiecare, aliniate una lângă alta. O formaţiune cristalizabilă este alcătuită din $3$ molecule de acelaşi tip, învecinate două câte două, având una dintre cele patru forme din imaginea alăturată (fig. 1).

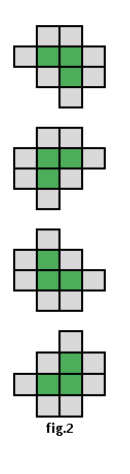
Fiecare formaţiune este înconjurată de jur-împrejur, ca în fig. 2, de un înveliş special format şi el din molecule identice, de alt tip decât cele din formaţiunea cristalizabilă pe care o înconjoară şi o izolează de restul formaţiunilor moleculare. În acest fel, fiecare moleculă din formaţiunea cristalizabilă se învecinează la Nord, Sud, Est şi Vest cu o moleculă din aceeaşi formaţiune cristalizabilă sau cu o moleculă din învelişul special.
Fiecare formaţiune cristalizabilă se bombardează cu raze $X$ şi în acest fel are loc cristalizarea, proces prin care învelişul special se extinde peste formaţiunea cristalizabilă pe care o înconjoară, formând o singură structură din care se va dezvolta cristalul.

Cerinţă

1. Determinaţi numărul formaţiunilor cristalizabile ce pot fi identificate pe eşantionul analizat.
2. Afişaţi eşantionul rezultat după cristalizare.

Date de intrare

Fişierul de intrare cristale.in conţine pe prima linie un număr natural $c$ reprezentând cerinţa care trebuie să fie rezolvată ($1$ sau $2$). Pe cea de-a doua linie se află două numere naturale $M$ şi $N$, separate printr-un spaţiu, având semnificaţia din enunţ. Pe următoarele $M$ linii se află câte $N$ numere naturale, separate prin câte un spaţiu, reprezentând moleculele din eşantionul analizat.

Date de ieşire

Dacă valoarea lui $c$ este $1$, atunci se va rezolva numai cerinţa $1$, caz în care pe prima linie a fişierului cristale.out va fi scris un număr natural reprezentând numărul formaţiunilor cristalizabile identificate pe eşantionul analizat.
Dacă valoarea lui $c$ este $2$, atunci se va rezolva numai cerinţa $2$. În acest caz, fişierul de ieşire cristale.out va conţine pe fiecare dintre primele $M$ linii, câte $N$ numere naturale separate prin câte un spaţiu, reprezentând moleculele eşantionului rezultat după cristalizare.

Restricţii şi precizări

• $4 \leq M, N \leq 800$ şi tipul fiecărei molecule este exprimat printr-un număr natural din intervalul $[1, 16]$;
• pe marginea eşantionului nu pot fi identificate formaţiuni cristalizabile;
• există cel puţin o formaţiune cristalizabilă pe eşantionul analizat;
• eşantionul nu conţine formaţiuni cristalizabile lipite (cu celule vecine pe una din cele patru direcţii);
• pentru rezolvarea corectă a cerinţei $1$ se acordă $30\%$ din punctaj, iar pentru rezolvarea corectă a cerinţei $2$ se acordă $70\%$ din punctaj.

Exemplul 1

cristale.in

1
6 8
5 6 6 1 5 2 6 5
6 9 9 6 1 7 1 2
6 6 9 6 3 4 1 6
2 2 6 3 4 7 4 2
8 8 2 4 7 7 4 6
8 2 7 2 4 4 2 5

cristale.out

2

Explicație

Se va rezolva cerinţa $1$ a problemei.
Eşantionul are $6$ rânduri cu câte $8$ molecule pe fiecare rând. Pe acest eşantion observăm o formaţiune cristalizabilă cu celule de tip $9$, izolată de învelişul special format din celule identice, toate de tip $6$ şi o formaţiune cristalizabilă cu celule de tip $7$, izolată de învelişul special format din celule identice, toate de tip $4$. Formaţiunea de $3$ molecule de tip $8$ nu este o formaţiune cristalizabilă întrucât se află pe marginea eşantionului.

Exemplul 2

cristale.in

2
6 8
5 6 6 1 5 2 6 5
6 9 9 6 1 7 1 2
6 6 9 6 3 4 1 6
2 2 6 3 4 7 4 2
8 8 2 4 7 7 4 6
8 2 7 2 4 4 2 5

cristale.out

5 6 6 1 5 2 6 5
6 6 6 6 1 7 1 2
6 6 6 6 3 4 1 6
2 2 6 3 4 4 4 2
8 8 2 4 4 4 4 6
8 2 7 2 4 4 2 5

Explicație

Se va rezolva cerinţa $2$ a problemei.
După cristalizare, peste fiecare din cele două formaţiuni cristalizabile identificate se extinde învelişul din jurul lor.