Tudor a primit un joc educaţional numit “Roboţel” cu ajutorul căruia va învăţa punctele cardinale Nord, Est, Sud, Vest. Jocul constă dintr-un roboţel care se deplasează pe o tablă de forma unei matrici pătratice, împărţită în linii şi coloane. Fiecare căsuţă, aflată la intersecţia dintre o linie şi o coloană, este fie căsuță „liberă”, fie căsuță semnalizator, caz în care este etichetată cu una din literele N, E, S, V, reprezentând sensuri posibile de deplasare. Când roboțelul ajunge într-o „căsuţă semnalizator”, el îşi schimbă sensul de deplasare astfel:
- Dacă căsuţa este etichetată cu
Natunci roboţelul se va deplasa în continuare de jos în sus - Dacă căsuţa este etichetată cu
Eatunci roboţelul se va deplasa în continuare de la stânga la dreapta - Dacă căsuţa este etichetată cu
Satunci roboţelul se va deplasa în continuare de sus în jos - Dacă căsuţa este etichetată cu
Vatunci roboţelul se va deplasa în continuare de la dreapta la stânga
Două căsuțe semnalizator formează o pereche blocantă dacă:
- Se află pe aceeași linie și conțin literele
EșiV, căsuța cuEare coloana mai mică decât a celei etichetate cuVși între ele, pe aceeași linie nu există alte căsuțe semnalizatoare. - Se află pe aceeași coloană și conțin literele
SșiN, căsuța cuSare linia mai mică decât a celei etichetate cuNși între ele, pe aceeași coloană nu există alte căsuțe semnalizatoare.

În , de exemplu, sunt perechi blocante: Perechea , și perechea , . Roboţelul porneşte din căsuţa , aflată pe prima linie și prima coloană şi dacă aceasta este liberă, se deplasează, în cadrul primei linii, de la stânga la dreapta. În cazul în care căsuța de pornire este semnalizator, atunci roboțelul se va deplasa pe direcția indicată de litera cu care este etichetată.
Considerând că roboțelul se deplasează pe tablă, el se oprește doar în următoarele situații:
- Roboţelul intră într-o căsuţă liberă aflată pe prima sau ultima linie, respectiv prima sau ultima coloană, caz în care dacă s-ar menține sensul deplasării actuale roboțelul ar părăsi tabla
- Roboțelul intră într-o „căsuţă semnalizator” a unei perechi blocantă și se va opri în cealaltă căsuță a perechii
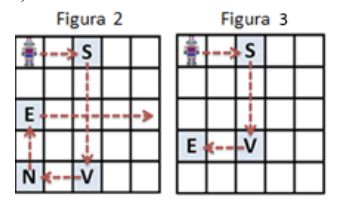
De exemplu, în , roboțelul ajunge în căsuța liberă unde se oprește. În , roboțelul se va opri în căsuța deoarece dacă ar schimba sensul spre Est, ar reveni în ultima căsuță semnalizator vizitată, .
Roboțelul înaintează o căsuță într-un pas, în sensul de deplasare.
Cerinţe
Scrieţi un program care, cunoscând numărul de linii şi coloane și cele căsuţe semnalizator, determină:
- Toate perechile blocante de pe tablă
- Numărul de pași efectuați pe fiecare sens în parte: Nord, Est, Sud și Vest
Date de intrare
Fişierul de intrare robotel.in conţine pe prima linie numărul natural reprezentând cerința din problemă care trebuie rezolvată, pe a doua linie, separate printr-un spaţiu numărul natural şi numărul natural , iar pe următoarele linii, două numere naturale și un caracter, separate prin câte un spațiu reprezentând, în ordine, linia, coloana şi litera unei căsuţe semnalizator.
Date de ieşire
Dacă valoarea lui este , se va rezolva doar cerința . Fişierul de ieşire robotel.out va conține perechile blocante, pentru fiecare pereche de căsuțe afișându-se numere naturale separate printr-un spaţiu, reprezentând, în ordine, linia, coloana primei căsuțe semnalizator, respectiv linia și coloana celei de-a doua căsuțe semnalizator. Perechile de căsuțe vor fi afișate pe linii ordonat după regula: o pereche va fi afișată înaintea perechii dacă sau și , adică se va afișa mai întâi perechea cu prima căsuță având linia mai mică decât a primei căsuțe din cealaltă pereche sau la linii egale, va fi afișată perechea cu coloana mai mică. Dacă nu există astfel de perechi de căsuțe, în fișierul de ieșire se va afișa valoarea .
Dacă valoarea lui este , se va rezolva doar cerința . Fişierul de ieşire robotel.out va conţine numere naturale separate printr-un spaţiu, reprezentând, în ordine, numărul de pași parcurși de roboţel în sensurile Nord, Est, Sud, și Vest.
Restricţii şi precizări
- Pentru rezolvarea corectă a fiecărei cerinţe se obțin câte de puncte
- O căsuță semnalizator conține o singură literă
- Pentru cerința se garantează că în toate testele deplasarea roboțelului se oprește!
Exemplul 1
robotel.in
1
5 4
1 3 S
3 1 E
5 1 N
5 3 V
robotel.out
0
Explicaţie
Nu există perechi blocante pe tablă care ar putea opri roboţelul.
Exemplul 2
robotel.in
1
5 3
1 3 S
4 1 E
4 3 V
robotel.out
4 1 4 3
Explicaţie
Perechea blocantă este alcătuită din căsuțele cu eticheta E și cu eticheta V. Dacă roboțelul ajunge în una dintre aceste căsuțe, atunci acesta se va opri în cealaltă căsuță.
Exemplul 2
robotel.in
1
5 5
1 3 S
2 5 S
4 1 E
4 3 V
5 5 N
robotel.out
2 5 5 5
4 1 4 3
Explicaţie
Căsuţa semnalizator de pe linia , coloana are eticheta S, iar căsuţa semnalizator de pe linia , coloana are eticheta N. Dacă roboțelul ajunge în una dintre aceste căsuțe, atunci acesta se va opri în cealaltă căsuță. Acelaşi lucru se întâmplă pentru căsuţa cu litera E de pe linia , coloana şi căsuţa cu litera V de pe linia , coloana .
Exemplul 3
robotel.in
1
5 5
1 2 S
2 1 E
2 3 E
2 5 V
5 2 N
robotel.out
1 2 5 2
2 3 2 5
Explicaţie
Prima pereche blocantă este , .
A doua pereche blocantă este , . Perechea , nu este validă deoarece conține un alt semnalizator între ele (vezi ).
Exemplul 4
robotel.in
2
5 3
1 3 S
4 1 E
4 3 V
robotel.out
0 2 3 2
Explicaţie
Numărul de pași efectuați pe sensul:
Nord: pași
Est: pași în căsuțele ,
Sud: pași în căsuțele , ,
Vest: pași în căsuțele ,
Exemplul 5
robotel.in
2
5 4
1 3 S
3 1 E
5 1 N
5 3 V
robotel.out
2 6 4 2
Explicaţie
Numărul de pași efectuați pe sensul:
Nord: pași în căsuțele ,
Est: pași în căsuțele , , , , ,
Sud: pași în căsuțele , , ,
Vest: pași în căsuțele ,