teren

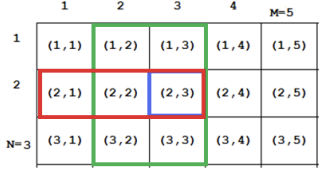
În satul vecin există un teren agricol de formă dreptunghiulară împărțit în $N \cdot M$ pătrate elementare identice, dispuse alăturat câte $M$ pe fiecare rând şi câte $N$ pe fiecare coloană. Rândurile sunt numerotate de la $1$ la $N$, iar coloanele de la $1$ la $M$. Un pătrat elementar situat în teren pe rândul $R$ și coloana $C$ este identificat prin coordonatele $(R, C)$.
Suprafețe dreptunghiulare din teren (formate fiecare din unul sau mai multe pătrate elementare alăturate) sunt revendicate de $T$ fermieri din sat, în calitate de moștenitori, pe baza actelor primite de la strămoșii lor. Pentru că au apărut și acte false, s-a constat că pot exista mai mulți fermieri care revendică aceleași pătrate elementare.
În cele $T$ acte ale fermierilor, suprafețele dreptunghiulare sunt precizate fiecare prin câte două perechi de numere $(X, Y)$ și $(Z, U)$, reprezentând coordonatele primului pătrat elementar din colțul stânga-sus al suprafeței (rândul $X$ și coloana $Y$), respectiv coordonatele ultimului pătrat elementar situat în colțul dreapta-jos al suprafeței (rândul $Z$ și coloana $U$).

Cerinţă

Scrieţi un program care să citească numerele naturale $N, M, T, R, C$ apoi cele $T$ perechi de coordonate $(X, Y)$ și $(Z, U)$ precizate în acte (corespunzătoare suprafețelor dreptunghiulare revendicate) și care să determine:

1. numărul fermierilor care revendică pătratul elementar identificat prin coordonatele $(R, C)$
2. numărul maxim de fermieri care revendică același pătrat elementar
3. numărul maxim de pătrate elementare ce formează o suprafață pătratică nerevendicată de niciun fermier

Date de intrare

Fişierul de intrare teren.in conţine pe prima linie un număr natural $P$ care poate avea doar valoarea $1$, valoarea $2$ sau valoarea $3$. Pe a doua linie a fișierului sunt scrise cinci numere naturale $N, M, T, R, C$, separate prin câte un spaţiu, cu semnificaţia din enunţ. Pe fiecare din următoarele $T$ linii ale fișierului sunt câte patru numere naturale nenule $X_K, Y_K, Z_K, U_K$, separate prin câte un spaţiu, reprezentând perechile de coordonate $(X_K,Y_K)$ și $(Z_K,U_K)$ corespunzătoare terenurilor revendicate de cei $T$ fermieri ($1 \leq K \leq T$).

Date de ieşire

Fişierul de ieşire teren.out va conţine pe prima linie un număr natural reprezentând numărul fermierilor care revendică pătratul elementar identificat prin coordonatele $(R, C)$ dacă cerința a fost $1$, un număr natural reprezentând numărul maxim de fermieri ce revendică același pătrat elementar dacă cerința a fost $2$, respectiv un număr natural reprezentând numărul maxim de pătrate elementare ce formează o suprafață pătratică nerevendicată de niciun fermier dacă cerința a fost $3$.

Restricţii şi precizări

• $3 \leq N, M \leq 180$
• $3 \leq T \leq 100$
• $1 \leq R \leq N$
• $1 \leq C \leq M$;
• $1 \leq X_K \leq Z_K \leq N$ şi $1 \leq Y_K \leq U_K \leq M$ pentru $1 \leq K \leq T$
• Pentru rezolvare corectă a cerinţei $1$ se acordă $20\%$ din punctaj, pentru rezolvarea corectă a cerinţei $2$ se acordă $20\%$ din punctaj, iar pentru rezolvarea corectă a cerinței $3$ se acordă $60\%$ din punctaj

Exemplul 1

teren.in

1
3 5 3 2 2
2 3 2 3
1 2 3 3
2 1 2 3

teren.out

2

Explicaţie

Pătratul elementar cu coordonatele $R = 2$ și $C = 2$ este revendicat de $2$ fermieri.

Exemplul 2

teren.in

2
3 5 3 2 2
2 3 2 3
1 2 3 3
2 1 2 3

teren.out

3

Explicaţie

Pătratul elementar cu coordonatele $(2, 3)$ este revendicat de $3$ fermieri (numărul maxim de revendicări).

Exemplul 3

teren.in

3
3 5 3 2 2
2 3 2 3
1 2 3 3
2 1 2 3

teren.out

4

Explicaţie

Sunt două suprafețe pătratice nerevendicate de niciun fermier, formate fiecare din numărul maxim de patru pătrate elementare. Acestea au coordonatele: $(1, 4)$ și $(2, 5)$ respectiv $(2, 4)$ și $(3, 5)$.