solitar

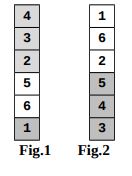
Se consideră un joc de cărţi cu un număr nelimitat de coloane. Iniţial, pe prima coloană există, într‑o ordine oarecare, $N$ cărţi cu numere distincte din mulţimea ${1, 2, \dots, N}$, următoarele coloane fiind vide (fără cărţi). Numim secvenţă de la sfârşitul coloanei ultima sau ultimele două sau ultimele trei etc. cărţi din coloană care au scrise pe ele numere consecutive în ordine crescătoare, considerate de jos în sus. De exemplu, în figurile $1$ şi $2$ sunt reprezentate două astfel de coloane cu câte $6$ cărţi având numere între $1$ şi $6$. În figura $1$, secvenţa de la sfârşitul coloanei este formată doar din cartea $1$. În figura $2$, secvenţa de la sfârşitul coloanei este formată din cărţile $3$, $4$ şi $5$. Se observă că în coloana din figura $1$ mai există o secvenţă formată din cărţile $2$, $3$ şi $4$, dar aceasta nu este la sfârşitul coloanei.

Operaţiile permise ale jocului sunt:

• $A$. mutarea secvenţei de cărţi de la sfârşitul unei coloane pe o coloană nouă, dacă acea coloană este vidă (nu conţine nicio carte);
• $B$. mutarea secvenţei de cărţi de la sfârşitul unei coloane la sfârşitul altei coloane cu cărţi, doar dacă secvenţa mutată formează o secvenţă de numere consecutive cu cele de pe cartea sau cărţile aflate la sfârşitul coloanei respective.

Se doreşte ca, printr-un număr minim de operaţii permise, să se obţină pe una dintre coloane toate numerele de la $1$ la $N$, în ordine crescătoare, considerate de jos în sus.

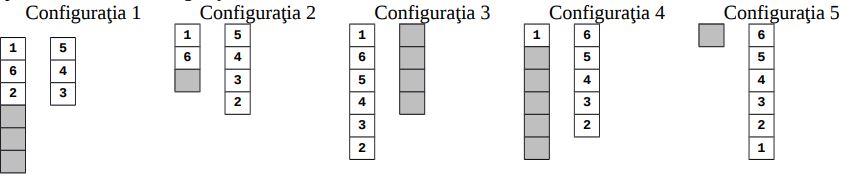
De exemplu, de la configuraţia iniţială din figura $2$ se va obţine, printr-o operaţie $A$, configuraţia $1$ de mai jos. Apoi, printr-o operaţie $B$, se obţine configuraţia $2$, printr-o nouă operaţie $B$ se obţine configuraţia $3$, apoi se mută secvenţa $2,3,4,5,6$ pe o coloană vidă (operaţia $A$), apoi se mută secvenţa $1$ peste secvenţa $2,3,4,5,6$ (operaţia B) şi se obţine, pe coloana a doua, configuraţia finală cerută.

Cerință

Cunoscând valoarea lui $N$, precum şi valorile cărţilor de pe prima coloană, să se determine numărul minim de operaţii prin care se poate obţine secvenţa $1, 2, \dots, N$ pe una dintre coloane.

Date de intrare

Fişierul solitar.in conţine pe prima linie numărul natural $N$ şi pe linia următoare N numere naturale distincte din mulţimea ${1, 2, \dots, N}$, separate prin câte un spaţiu, date în ordinea de pe coloană, de sus în jos.

Date de ieșire

Fişierul solitar.out va conţine o singură linie pe care va fi scris un număr natural $M$ reprezentând numărul minim de operaţii prin care se poate obţine secvenţa cerută.

Restricții și precizări

• $1 \leq N \leq 100 \ 000$

Exemplu

solitar.in

6
1 6 2 5 4 3

solitar.out

5

Explicație

Cele $5$ mutări sunt descrise în enunţul problemei.