iepurasi

Se construieşte un şir de numere naturale care respectă restricţiile:

• primul număr din şir este $9$;
• numerele se generează în ordine strict crescătoare;
• şirul conţine toate numerele formate doar cu cifrele $7$, $8$ şi $9$ cu proprietatea că numărul cifrelor $9$ este mai mare sau egal decât numărul cifrelor $8$ şi numărul cifrelor $8$ este mai mare sau egal decât numărul cifrelor $7$.

Primii $14$ termeni ai şirului, în ordine, sunt: $9$, $89$, $98$, $99$, $789$, $798$, $879$, $897$, $899$, $978$, $987$, $989$, $998$, $999$.
Pornind de la aceste numere, Liv a inventat un joc interactiv: $N$ iepuraşi sunt aşezaţi în şir, fiecare având câte un cartonaş. Fiecare cartonaş are două feţe, o faţă albă pe care este inscripţionat un număr din acest şir şi o faţă gri, pe care este inscripţionată poziţia acelui număr în şir, poziţii numerotate în ordine, începând cu valoarea $1$.

Exemple. Cartonaşul care are pe faţa gri inscripţionat numărul $1$ va avea pe faţa albă inscripţionat numărul $9$, iar cartonaşul care are pe faţa gri inscripţionat numărul $5$ va avea pe faţa albă inscripţionat numărul $789$.
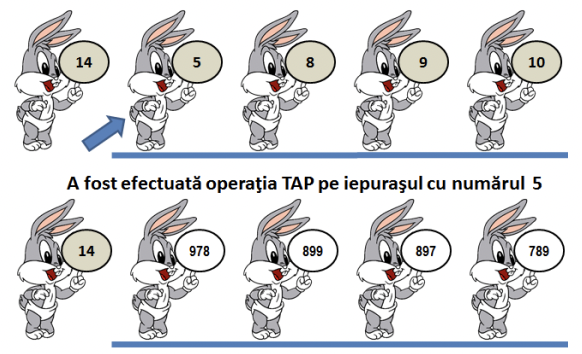
Iepuraşii sunt aşezaţi într-o ordine oarecare şi ţin cartonaşele astfel încât să se vadă faţa gri. Jocul constă în a rearanja iepuraşii de la stânga la dreapta, descrescător după numerele inscripţionate pe feţele gri, având la dispoziţie doar operaţia $TAP$ pe un iepuraş. Când se aplică operaţia $TAP$ unui iepuraş atunci secvenţa de iepuraşi, începând de la cel pe care s-a făcut $TAP$ şi până la sfârşitul şirului (spre dreapta), este oglindită (ca în imaginea din dreapta). După oglindire, toţi iepuraşii din acea secvenţă ţin cartonaşele astfel încât să se vadă faţa albă. Se doreşte aplicarea unui număr cât mai mic de operaţii $TAP$ pentru rearanjarea iepuraşilor.

Cerinţe

Scrieţi un program care să citească numerele naturale $N$ (reprezentând numărul de iepuraşi) şi $a_1$, $a_2$, $\dots$, $a_N$ (reprezentând, în ordine, numerele inscripţionate pe feţele gri) și care să determine:

1. Numărul minim de operaţii $TAP$ necesare rearanjării iepuraşilor;
2. Cel mai mic număr aflat pe o faţă albă care nu se vede, în cazul în care au rămas cartonaşe neîntoarse. Dacă toate cartonaşele au fost întoarse (la toate fiind vizibilă faţa albă) se va afişa cel mai mare număr aflat pe o faţă albă a unui cartonaş.

Date de intrare

Fişierul de intrare iepurasi.in conţine pe prima linie numărul natural $N$ reprezentând numărul de iepuraşi. A doua linie a fişierului conţine, în ordine, cele $N$ numere: $a_1$, $a_2$, $\dots$, $a_N$, separate prin câte un spaţiu, reprezentând în ordine, numerele inscripţionate pe feţele gri ale cartonașelor.

Date de ieşire

Fişierul de ieşire iepurasi.out va conţine pe prima linie un număr reprezentând numărul minim de operaţii $TAP$ necesare rearanjării iepuraşilor. A doua linie va conține un număr reprezentând cel mai mic număr aflat pe o faţă albă care nu se vede (în cazul în care au rămas cartonaşe neîntoarse), respectiv cel mai mare număr aflat pe o faţă albă a unui cartonaş, în cazul în care toate cartonaşele au fost întoarse (la toate fiind vizibilă faţa albă).

Restricţii și precizări

• $2 \leq N \leq 10 \ 000$;
• $1 \leq a_i \leq 10 \ 000$ ($1 \leq i \leq N$);
• $N$, $a_1$, $a_2$, $...$, $a_N$ sunt numere naturale;
• pentru rezolvarea cerinţei $1$ se acordă $50\%$ din punctaj, iar pentru cerinţa $2$ se acordă $50\%$ din punctaj.

Exemple

iepurasi.in

5
14 5 8 9 10

iepurasi.out

1
999

Explicaţie

Se aplică o singură operaţie $TAP$ pe iepuraşul cu numărul de ordine $5$. Cartonaşul neîntors are numărul de ordine $14$ ($999$).