babilon

Babilonienii au dezvoltat un sistem pozițional de scriere a numerelor, în care orice număr natural se poate reprezenta utilizând semnele:

Semn	Cifra
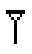	unu
	zece

Valorile $k$ din {$2$, $3$, $...$, $9$} se obțin scriind semnul pentru unu de $k$ ori
Exemplu: scrierea babiloniană a lui $3$ este

Numerele $11$, $12$, $\dots$, $59$ se obțin ca succesiuni de semne urmate de semne
Exemplu: $43$ se reprezintă ca

Sistemul folosește gruparea unităților câte șaizeci. Astfel, pentru a scrie numărul șaizeci se folosește același semn ca pentru unu, dar valoarea sa este dată de poziția în care se găsește semnul.
Babilonienii nu foloseau cifra $0$. Pentru poziţionarea corectă a semnelor se utiliza spațiu:

Exemple:

Număr	Reprezentare
$60$
$3600$

Se codifică scrierea babiloniană a unui număr astfel:

Cifră	Semn
$1$
$2$
$3$

Exemple:

Scrierea babiloniană	Codificarea scrierii babiloniene	Valoarea zecimală a numărului
	$1311$	$1 \cdot 60 + 2 = 62$
	$12$	$1 \cdot 60 + 10 = 70$
	$1221111$	$1 \cdot 60 + 20 + 4 = 84$
	$1231111$	$1 \cdot 60 \cdot 60 + 10 \cdot 60 + 3 = 4203$

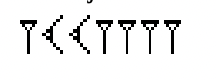Cerință

Dându-se un număr natural $n$ și un șir de $n$ cifre dintre {$1$, $2$, $3$}, reprezentând codificarea scrierii babiloniene a unui număr natural, să se determine:

1. numărul maxim de cifre $1$ aflate pe poziții consecutive în codificarea scrierii babiloniene date;
2. numărul natural din sistemul zecimal corespunzător scrierii babiloniene date.

Date de intrare

Fișierul de intrare babilon.in va conține:

• pe prima linie un număr natural $p$ ($1 \leq p \leq 2$);
• pe a doua linie un număr natural $n$;
• pe a treia linie $n$ cifre separate prin câte un spațiu, reprezentând codificarea scrierii babiloniene a unui număr natural.

Date de ieșire

Dacă valoarea lui $p$ este $1$, atunci se va rezolva numai punctul $1$ din cerință. În acest caz, fişierul de ieşire babilon.out va conţine pe prima linie un număr natural reprezentând numărul maxim de cifre $1$ aflate pe poziții consecutive în codificarea scrierii babiloniene date.
Dacă valoarea lui $p$ este $2$, atunci se va rezolva numai punctul $2$ din cerință. În acest caz, fişierul de ieşire babilon.out va conţine pe prima linie numărul natural corespunzător scrierii babiloniene date.

Restricţii şi precizări

• $2 \leq n \leq 109$;
• se garantează faptul că numărul de cifre al rezultatului de la punctul $2$ (numărul zecimal) este mai mic decât $20$;
• $30\%$ din teste vor avea pe prima linie valoarea $1$, iar restul de $70\%$ din teste vor avea pe prima linie valoarea $2$.

Exemplul 1

babilon.in

1
8
1 1 3 2 1 1 1 2

babilon.out

3

Explicație

$1 \ 1 \ 3 \ 2$ 1 1 1 $2$
Cea mai lungă secvență de cifre $1$ are lungimea $3$.

Exemplul 2

babilon.in

2
7
1 1 3 2 1 1 1

babilon.out

7213

Explicație

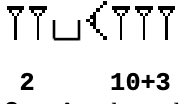
$2$ se înmulțește de două ori cu $60$ (o dată pentru că este urmat de spațiu și încă o dată pentru că precede o grupă care începe cu semnul pentru zece), apoi se adună valoarea $13$.
$2 \cdot 60 \cdot 60 + 10 + 3 = 7213$

Exemplul 3

babilon.in

2
9
1 1 1 2 1 1 2 2 1

babilon.out

11541

Explicație

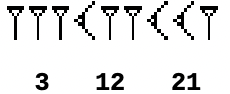
$3$ se înmulțește cu $60$ de două ori pentru că este precedat de două grupe care încep cu semnul pentru zece, apoi se adună $12$ înmulţit cu $60$ şi la final se adună $21$.
$3 \cdot 60 \cdot 60 + 12 \cdot 60 + 21 = 11541$