Într-un oraș există un hotel de formă cubică, cu etaje, numerotate de la la . Suprafața fiecărui etaj este pătratică și este împărțită în camere identice alăturate, dispuse pe linii și coloane, fiecare cameră având drept etichetă un triplet de numere naturale ( este etajul, este linia, este coloana, ), ca în imaginea alăturată.
Dintre cele camere ale hotelului, una este specială deoarece în ea locuiește de mult timp un șoricel. Fiind isteț, el știe eticheta camerei în care se află precum și eticheta camerei în care bucătarul hotelului depozitează alimente.

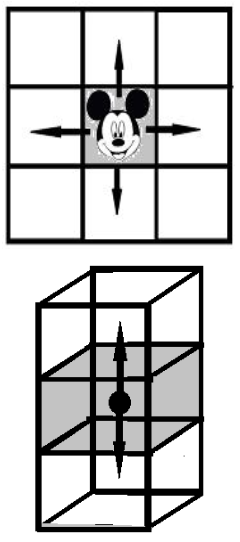 Studiind hotelul, șoricelul a constatat că pe fiecare etaj, din orice cameră poate intra în toate camerele care au un perete comun cu aceasta (existând un mic orificiu pentru aerisire).
Studiind hotelul, șoricelul a constatat că pe fiecare etaj, din orice cameră poate intra în toate camerele care au un perete comun cu aceasta (existând un mic orificiu pentru aerisire).
De asemenea, șoricelul a constatat că din orice cameră poate intra în camera situată imediat deasupra ei (dacă există) și în camera situată imediat sub ea (dacă există).
Fiind un șoricel binecrescut, el nu intră în nicio cameră ocupată de clienți ca să nu-i deranjeze.
Hotelul având mulți clienți, șoricelul trebuie să-și găsească cel mai scurt traseu de la camera lui la camera cu alimente, traseu care să treacă printr-un număr minim de camere, toate neocupate.
Cerință
Se cere să se determine:
- numărul de camere prin care trece cel mai scurt traseu al șoricelului de la camera lui la camera cu alimente (inclusiv camera lui şi camera cu alimente);
- etichetele camerelor prin care trece traseul determinat la punctul 1.
Date de intrare
Fişierul traseu.in conţine:
- pe prima linie, două numere naturale și separate printr-un spațiu, cu semnificația din enunț iar reprezentând numărul de camere ocupate de clienţii hotelului;
- pe a doua linie, trei numere naturale , , , separate prin câte un spațiu, reprezentând eticheta camerei în care se află șoricelul;
- pe a treia linie, trei numere naturale , , , separate prin câte un spațiu, reprezentând eticheta camerei în care sunt depozitate alimentele;
- pe fiecare dintre următoarele linii, câte trei numere naturale , , , separate prin câte un spaţiu, reprezentând etichetele celor camere ocupate de clienți.
Date de ieșire
Fişierul de ieşire traseu.out va conţine pe prima linie un număr natural reprezentând numărul de camere prin care trece cel mai scurt traseu al șoricelului de la camera lui la camera cu alimente determinat la punctul 1. Pe fiecare din următoarele linii, se vor scrie câte trei numere naturale , , , separate prin câte un spaţiu, reprezentând etichetele camerelor prin care trece traseul determinat la punctul 1, în ordinea în care sunt parcurse camerele de către șoricel pentru a ajunge din camera lui în camera cu alimente.
Restricții și precizări
- Șoricelul nu intră decât în camere neocupate de clienți.
- Camera șoricelului este o cameră neocupată de clienți.
- Dacă există mai multe trasee ale șoricelului de la camera lui la camera de alimente care trec prin exact camere, atunci traseul afișat va fi cel mai mic traseu din punct de vedere lexicografic.
- Eticheta se consideră strict mai mică în sens lexicografic ca eticheta dacă este satisfăcută doar una dintre condițiile:
- ;
- și ;
- și și .
- Eticheta se consideră egală cu eticheta dacă și și . Vom scrie egalitatea lor astfel: .
- Traseul ce trece (în această ordine) prin camerele cu etichetele , , ..., este mai mic din punct de vedere lexicografic ca traseul , , ..., dacă există un indice () astfel încât , , ..., iar eticheta este strict mai mică în sens lexicografic ca eticheta .
- Se acordă din punctaj pentru determinarea corectă a numărului și din punctaj pentru rezolvarea corectă a ambelor cerințe.
- Se garantează că există soluție pentru ambele cerințe, pentru toate datele de test.
Exemplu
traseu.in
3 4
1 1 1
3 3 3
3 3 1
2 1 1
3 1 1
3 1 3
traseu.out
7
1 1 1
1 1 2
1 1 3
1 2 3
1 3 3
2 3 3
3 3 3
Explicație
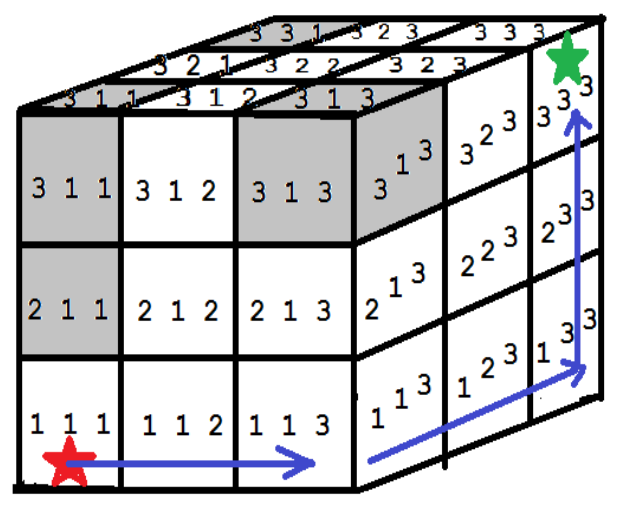 Hotelul are trei etaje (, şi ). Pe fiecare etaj sunt camere. Șoricelul se află în camera cu eticheta iar camera cu alimente are eticheta .
Hotelul are trei etaje (, şi ). Pe fiecare etaj sunt camere. Șoricelul se află în camera cu eticheta iar camera cu alimente are eticheta .
Sunt camere ocupate de clienţi. Acestea au etichetele: , , , . Traseul cel mai scurt trece prin camere. Sunt mai multe astfel de trasee. Câteva exemple:
- , , , , , , ;
- , , , , , , ;
- , , , , , , ;
Traseul 1 din lista de mai sus este cel mai mic în sens lexicografic.