domino

Ionel are $n$ piese de domino de diverse înălţimi. În joacă, el aşează piesele vertical într-un şir (pe o riglă gradată), la distanţe nu neapărat egale una faţă de alta. Ionel atinge prima piesă, aceasta cade şi poate antrena în cădere după ea şi alte piese din şir. Dacă mai rămân piese în picioare, el merge la prima piesă care nu a căzut şi o atinge. Aceasta cade şi poate antrena în cădere după ea şi alte piese. Continuă procedeul până când nu mai rămâne nicio piesă în picioare.

Cerinţă

Scrieţi un program care să citească numărul natural $n$ de piese, poziţia pe riglă şi înălţimea fiecărei piese, în această ordine, şi care să determine numărul minim necesar de atingeri ale pieselor astfel încât să cadă toate piesele de domino precum şi numărul maxim de piese răsturnate la o singură atingere.

Date de intrare

Fişierul de intrare domino.in conţine:

• pe prima linie, numărul natural $n$
• pe fiecare dintre următoarele $n$ linii câte două numere naturale $p$ şi $h$, separate printr-un spaţiu, $p$ reprezentând pozitia piesei pe riglă şi $h$ înălţimea piesei de domino, în acestă ordine.

Date de ieşire

Fişierul de ieşire domino.out va conţine o singură linie pe care sunt scrise două numere naturale $a$ şi $b$, în această ordine, separate printr-un spaţiu, $a$ reprezentând numărul minim necesar de atingeri ale pieselor, iar $b$ numărul maxim de piese ce sunt răsturnate la o singură atingere a unei piese.

Restricţii şi precizări

• Numerele $n$, $p$ şi $h$ sunt numere naturale nenule
• $1 \leq n \leq 1 \ 000$
• $1 \leq p \leq 5 \ 000$
• $1 \leq h \leq 5 \ 000$
• O piesă de domino aflată pe pozitia $p$ de înălţime $h$ răstoarnă piese până la poziţia $p + h$ inclusiv.
• În fişierul de intrare datele sunt în ordinea crescătoare a poziţiei pieselor de domino.
• Pe o poziţie de pe riglă se poate afla o singură piesă de domino.
• Ionel începe întotdeauna cu piesa aşezată la poziţia cea mai mică
• Se acordă $50\%$ din punctaj pentru rezolvarea corectă a fiecărei cerinţe.

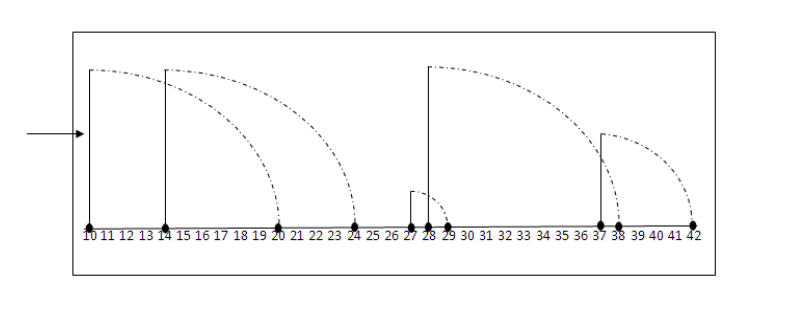
Exemplu

domino.in

5
10 10
14 10
27 2
28 10
37 5

domino.out

2 3

Explicaţie

La atingerea primei piese vor cădea primele două piese;
Atingea piesei de pe poziţia $27$ răstoarnă piesa de pe poziţia $28$ iar aceasta o răstoarnă şi pe ultima
Numărul de atingeri este $2$ iar numărul maxim de piese doborâte la o atingere este $3$