magic

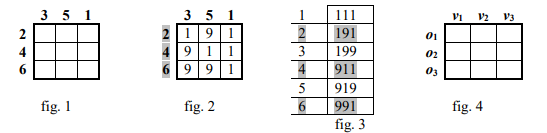
Se dă o matrice cu $n$ linii şi $n$ coloane. Coloanele şi liniile sunt etichetate cu numere de la $1$ la $2 \cdot n$, folosind fiecare număr câte o singură dată (fig. $1$ – exemplu pentru $n = 3$). Vom nota şirul etichetelor asociat liniilor matricei $o_1$, $o_2$, $\dots$, $o_n$, iar şirul etichetelor asociat coloanelor matricei cu $v_1$, $v_2$, $\dots$, $v_n$ (fig. $4$).

Trebuie să se completeze fiecare element al matricei cu una dintre cifrele $1$ sau $9$ (fig. $2$). Prin concatenarea cifrelor de pe o linie sau o coloană obţinem un număr de $n$ cifre. În total se obţin $2 \cdot n$ numere. Aceste numere trebuie să fie distincte două câte două şi aranjându-le în ordinea etichetelor asociate liniilor şi coloanelor trebuie să fie în ordine crescătoare (fig. $3$). Vom concatena cele $2 \cdot n$ numere în ordinea etichetelor şi obţinem un singur număr de $2 \cdot n^2$ cifre. Acest număr îl vom denumi cheie magică. Pentru exemplul din fig. $3$ obţinem cheia magică $111 \colorbox{blue}{191} \ 199 \colorbox{blue}{911} \ 919 \ \colorbox{blue}{991}$

Cerinţă

Se dau $x$ un număr natural, dimensiunea $n$ a matricei şi cele două şiruri de etichete $o_1$, $o_2$, $\dots$, $o_n$ respectiv $v_1$, $v_2$, $\dots$, $v_n$. Să se tipărească numărul de chei magice distincte (dacă $x = 1$) sau cea mai mică cheie magică ce se poate asocia matricei (dacă $x = 2$).

Date de intrare

Fişierul de intrare magic.in conţine patru linii. Pe linia $1$ se află numărul natural $x$ ($1$ sau $2$). Pe linia $2$ se află numărul natural $n$. Pe linia $3$ se află $n$ numere naturale distincte separate prin câte un spaţiu reprezentând şirul $o_1$, $o_2$, $\dots$, $o_n$ iar pe linia $4 - n$ numere naturale distincte separate prin câte un spaţiu reprezentând şirul $v_1$, $v_2$, $\dots$, $v_n$.

Date de ieșire

Fişierul de ieşire magic.out va conţine o singură linie pe care va fi scris un număr natural care reprezintă:

• dacă $x=1$, numărul cheilor magice distincte;
• dacă $x=2$, cea mai mică cheie magică.

Restricții și precizări

• $3 \leq n \leq 5$
• Pentru fiecare fişier test există cel puţin o soluţie.
• Pentru $50\%$ dintre teste $x=1$ (aflarea numărului de chei magice), iar pentru $50\%$, $x=2$ (aflarea celei mai mici chei magice)
• Pentru $20\%$ dintre teste $n=3$, $30\%$ dintre teste $n=4$ şi pentru $50\%$ dintre teste $n=5$.

Exemplul 1

magic.in

1
3
2 4 6
3 5 1

magic.out

3

Exemplul 2

magic.in

2
3
2 4 6
3 5 1

magic.out

111191199911919991

Explicații

Avem două soluţii:

1 9 1
9 1 1 
9 9 1

1 9 1
9 1 1
9 9 9

Numerele obţinute în ordinea etichetărilor: ($111$, $191$, $199$, $911$, $919$, $991$) respectiv ($119$, $191$, $199$, $911$, $919$, $999$).

Cele două chei magice sunt $111191199911919991$ respectiv $119191199911919999$, dintre care prima e mai mică.