cartonas

Avem la dispoziţie cartonaşe dreptunghiulare pe care sunt inscripţionate numere naturale şi o valoare dată $x$. Pornind de la un număr $N$ de astfel de cartonaşe, aşezate alăturat şi considerate a forma nivelul de bază (notat cu $1$), se formează următoarele $N - 1$ niveluri după regulile de mai jos (a se vedea şi figura din exemplu pentru clarificare):

• numărul de cartonaşe de pe un nivel oarecare este cu $1$ mai mic decât numărul de cartonaşe de pe nivelul imediat inferior
• numărul înscris pe orice cartonaş se obţine ca sumă a numerelor de pe cartonaşele peste care “se aşează”, cartonaşe aflate pe nivelul imediat inferior.

Pe fiecare nivel se calculează suma numerelor de pe toate cartonaşele. Se vor forma astfel $N$ sume care se reprezintă fiecare în baza $2$.

Exemplu:

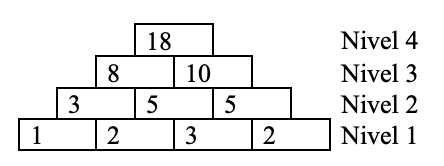
Cerinţă

1. Să se afişeze numărul inscripţionat pe cartonaşul de pe ultimul nivel.
2. Să se precizeze numărul nivelului pe care se află valoarea dată $x$
3. Să se afişeze numerele nivelelor în ordinea descrescătoare a numărului de cifre egale cu $1$ din reprezentarea în baza $2$ a sumei fiecărui nivel. Dacă există două nivele cu sumă având acelaşi număr de cifre egale cu $1$, se va afişa mai întâi nivelul cu numărul mai mic.

Date de intrare

În fişierul cartonas.in se află:

• pe prima linie un număr natural $N$ care reprezintă numărul de cartonaşe ce formează nivelul $1$ (nivelul de bază)
• pe a doua linie un număr natural $x$ care reprezintă valoarea căutată
• pe a treia linie se află cele $N$ numere de pe nivelul $1$ (de bază), separate două câte două printr-un spaţiu

Date de ieşire

În fişierul cartonas.out se va scrie:

• pe prima linie numărul inscripţionat pe cartonaşul de pe ultimul nivel
• pe linia a doua se va afişa nivelul pe care se află valoarea căutată $x$
• pe linia a treia se vor afişa numerele de nivel în ordinea cerută, separate două câte două printr-un spaţiu

Restricţii şi precizări

• $1 \leq N \leq 100$
• $x$ este număr natural de maxim $7$ cifre
• Valorile de pe cartonaşe sunt numere naturale de maxim $7$ cifre
• Se ştie că există suficiente cartonaşe cu inscripţia oricărui număr necesar, numerele de pe nivelul de bază nu conduc la numere pe celelalte nivele care să aibă mai mult de $7$ cifre, iar sumele de pe fiecare nivel au maxim $9$ cifre.
• Se acordă punctaje parţiale: $30\%$ din punctaj pentru cerinţa $1$, $30\%$ din punctaj pentru cerinţa $2$ şi $40\%$ din punctaj pentru cerinţa $3$

Exemplu

cartonas.in

4
8
1 2 3 2

cartonas.out

18
3
2 3 4 1

Explicaţie

Pe ultimul nivel se va găsi valoarea $18$, iar valoarea $8$ se găseşte pe nivelul al treilea, conform desenului şi cerinţelor.
Pe primul nivel $S = 1 + 2 + 3 + 2 = 8 = 1000_{(2)}$, adică are $1$ cifră egală cu $1$
Pe cel de-al doilea nivel $S = 3 + 5 + 5 = 13 = 1101_{(2)}$, adică are $3$ cifre egale cu $1$
Pe cel de-al treilea nivel $S = 8 + 10 = 18 = 10010_{(2)}$, adică are $2$ cifre egale cu $1$
Pe cel de-al patrulea nivel $S = 18 = 10010_{(2)}$, adică are $2$ cifre egale cu $1$