Fi si Cri

După cum ştiţi din fabule, greieraşul $\text{Cri}$ ar vrea să o impresioneze cu interpretările sale artistice pe furnicuţa $\text{Fi}$. În povestea noastră, $\text{Fi}$ se află pe un teren de formă dreptunghiulară, format din $m$ şiruri de parcele (numerotate de la $1$ la $m$), pe fiecare şir fiind câte $n$ parcele (numerotate de la $1$ la $n$). Toate parcelele au acealeaşi dimensiuni şi în fiecare parcelă se află exact o firimitură. $\text{Fi}$ este iniţial în parcela $(a, b)$, pe şirul $a$, în poziţia $b$ şi urmează un traseu bine stabilit, de pe fiecare parcelă vizitată luând firimitura aflată în aceasta.
Prima parcelă pe care o vizitează când ajunge pe un şir este considerată reper al acelui şir. După ce vizitează reperul (de pe un şir oarecare $i$), ea vizitează mai întâi $k$ parcele aflate în stânga reperului, apoi se întoarce la reper pe drumul pe care a venit şi vizitează în continuare $k$ parcele aflate în dreapta reperului, după care merge pe şirul următor (şirul $i + 1$), reperul acestuia fiind chiar parcela alăturată celei pe care a vizitat-o ultima dată pe şirul anterior (şirul $i$), ca în desenul de mai jos. Pe fiecare şir $\text{Fi}$ procedează la fel, iar dacă la un moment dat numărul parcelelor din stânga sau dreapta reperului este mai mic decât $k$, pe acea direcţie vizitează numai parcelele pe care le are la dispoziţie până la limita terenului.

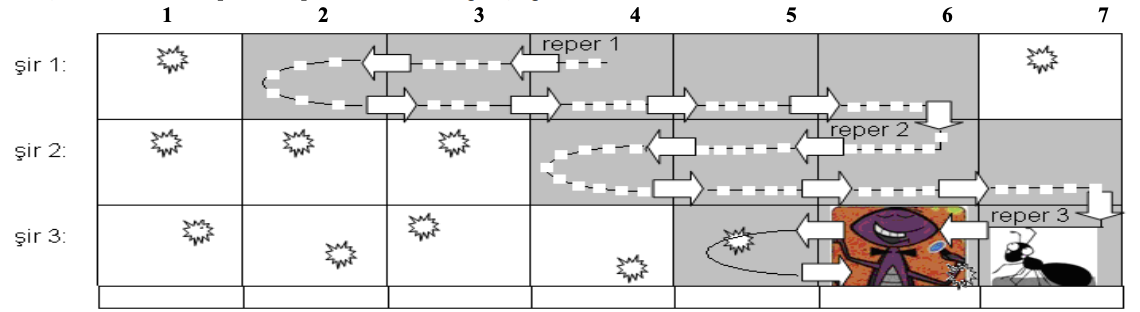
După ce a vizitat $p$ parcele, $\text{Fi}$ ajunge în parcela de coordonate $(c, d)$ unde îl întâlneşte pe perseverentul $\text{Cri}$, înarmat cu o colecţie de melodii de ultimă oră.

Cerinţă

Determinaţi şirul din care face parte şi numărul de ordine în şir al parcelei în care se află $\text{Cri}$ precum şi numărul total de firimituri, $t$, pe care le-a adunat în total $\text{Fi}$, până la întâlnirea cu $\text{Cri}$.

Date de intrare

În fişierul de intrare fi.in se află:

• pe prima linie $m$ şi $n$ (două numere naturale separate printr-un spaţiu)
• pe a doua linie $k$ şi $p$ (două numere naturale separate printr-un spaţiu)
• pe a treia linie $a$ şi $b$ (două numere naturale separate printr-un spaţiu)

Date de ieşire

În fişierul de ieşire fi.out se vor scrie

• pe prima linie, separate printr-un spaţiu, valorile $c$ şi $d$ (numărul şirului şi parcela din cadrul şirului în care se află $\text{Cri}$);
• pe a doua linie, valoarea $t$ (numărul total de firimituri adunate).

Restricţii şi precizări

• $1 \leq m, n \lt 10 ^ 9$
• $1 \leq k \leq \lfloor \frac{n}{2} \rfloor$
• $p \leq m \cdot n$
• $1 \leq a \leq m$
• $1 \leq b \leq n$

Exemplul 1

fi.in

4 7
2 17
1 4

fi.out

3 6
12

Explicație

Sunt $m = 4$ şiruri a câte $n = 7$ parcele. $\text{Fi}$ se deplasează cu $k = 2$ parcele în stânga şi în dreapta fiecărui reper, iar cele $17$ parcele parcurse sunt, în ordine: $(1, 4)$, $(1, 3)$, $(1, 2)$, $(1, 3)$, $(1, 4)$, $(1, 5)$, $(1, 6)$, $(2, 6)$, $(2, 5)$, $(2, 4)$, $(2, 5)$, $(2, 6)$, $(2, 7)$, $(3, 7)$, $(3, 6)$, $(3, 5)$, $(3, 6)$. A adunat $12$ firimituri (din parcelele subliniate mai sus).

Exemplul 2

fi.in

4 10
2 17
1 4

fi.out

1 7 
7

Explicație

Sunt $m = 4$ şiruri a câte $n = 10$ parcele. $\text{Fi}$ se deplasează cu $k = 5$ parcele în stânga şi în dreapta fiecărui reper, dar primul şir nu are suficiente parcele în stânga. Cele $10$ parcele parcurse sunt, în ordine: $(1, 4)$, $(1, 3)$, $(1, 2)$, $(1, 1)$, $(1, 2)$, $(1, 3)$, $(1, 4)$, $(1, 5)$, $(1, 6)$, $(1, 7)$. A adunat $7$ firimituri (din parcelele subliniate mai sus)