excursie

Gigel este un mare amator de excursii la munte. În acelaşi timp este şi un bun informatician. El a observat că făcând un traseu între două obiective turistice oboseşte mai puţin decât dacă alege un alt traseu între aceleaşi obiective. Gigel şi-a propus să găsească un model care să-i permită determinarea unui traseu pe care, dacă-l alege, va ajunge la destinaţie cât mai puţin obosit. Astfel, el reprezintă terenul în care se află cele două obiective turistice printr-un tablou bidimensional cu $n$ linii (numerotate de la $1$ la $n$) şi $m$ coloane (numerotate de la $1$ la $m$), cu elemente numere naturale strict pozitive, în care fiecare element reprezintă cota unei zone de teren de forma unui pătrat cu latura $1 \ m$. Efortul pe care-l face pentru a trece dintr-o zonă cu cota $c_1$ într-o zonă vecină cu o cotă mai înaltă ($c_2$) se calculează după cum urmează. Se trasează un triunghi dreptunghic ca în figură:

• $c_1$ şi $c_2$ sunt cele două cote, $c_1 < c_2$
• $1$ este distanţa dintre centrele celor două zone vecine
• $d = \sqrt{(c_2 - c_1)^2 + 1}$
• $\alpha$ este unghiul pantei care trebuie urcată

Apoi calculează efortul astfel: $ef = d \cdot tg \ \alpha$.

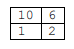
În exemplul următor considerăm patru zone vecine având cotele $1$, $2$, $6$, $10$. Pentru a ajunge din zona de cotă $1$ în zona de cotă $10$ se pot alege două trasee:

1. direct, ceea ce presupune un efort calculat astfel:
   • $ef = d \cdot tg \alpha = \sqrt{82} \cdot 9 \approx 81$.
2. ocolit, prin zonele de cote $2$ şi $6$, ceea ce presupune un efort calculat astfel:
   • $ef = ef_1 + ef_2 + ef_3 = \sqrt{2} + \sqrt{17} \cdot 4 + \sqrt{17} \cdot 4 \approx 34$.

Efortul pe care-l face pentru a trece dintr-o zonă având cota $c_1$ într-o zonă vecină cu aceeaşi cotă este $1$. Efortul pe care-l face pentru a trece dintr-o zonă având cota $c_1$ într-o zonă vecină cu o cotă mai joasă ($c_2$) este jumătate din efortul pe care l-ar face la urcare (adică de la cota $c_2$ la cota $c_1$).

Cerinţă

Scrieţi un program care să determine efortul minim pentru a ajunge de la un obiectiv turistic la altul, lungimea traseului nedepăşind o valoare dată $L_{max}$.

Date de intrare

Fişierul de intrare excursie.in conţine:

• pe prima linie două numere naturale $n$ şi $m$ separate printr-un spaţiu, reprezentând dimensiunile terenului;
• pe linia a doua numărul real $L_{max}$ reprezentând lungimea maximă admisă a drumului;
• următoarele $n$ linii conţin fiecare câte $m$ valori naturale, separate prin spațiu, reprezentând în ordine cotele zonelor de teren;
• ultima linie conţine patru valori naturale $l_i$, $c_i$, $l_f$, $c_f$, separate prin câte un spaţiu, unde $l_i$, $c_i$ reprezintă linia şi respectiv coloana punctului de plecare, iar $l_f$, $c_f$ reprezintă linia şi respectiv coloana punctului de sosire.

Date de ieșire

Fişierul de ieşire excursie.out va conţine pe prima linie două numere reale separate printr-un spaţiu $ef \ d$, reprezentând efortul minim depus pentru a ajunge de la un obiectiv la altul şi respectiv lungimea minimă a unui drum parcurs cu efort minim. Rezultatele vor fi afişate cu câte trei zecimale.

Restricții și precizări

• $2 \leq n, m \leq 50$
• Deplasarea dintr-o zonă în alta se poate face doar în $4$ direcţii: ($N$, $E$, $S$, $V$). Mai exact, dacă poziţia curentă este pe linia $i$, coloana $j$, prin deplasare la $N$ se trece în poziţia ($i-1, j$), la $E$ în ($i, j+1$), la $S$ în ($i+1, j$), iar la $V$ în ($i, j-1$). (dacă aceste poziţii există).
• Cotele sunt numere naturale cu valori între $1$ şi $100$.
• Se recomandă utilizarea tipurilor reale pe $64$ biţi. Rezultatul va fi considerat corect dacă diferenţa absolută dintre rezultatul afişat şi rezultatul corect este < $0.01$
• Se acordă $60\%$ din punctaj pentru determinarea corectă a efortului minim, respectiv $100\%$ pentru rezolvarea corectă a ambelor cerinţe

Exemplu

excursie.in

2 2
11
10 6
1 2
2 1 1 1

excursie.out

34.399 9.660

Explicație

$\sqrt{2} + 8 \cdot \sqrt{17} = 34.399 (1.41421356+32.98484500=34.39905856)$
$\sqrt{2} + 2 \cdot \sqrt{17} = 9.660 (1.41421356+ 8.24621125= 9.66042481)$

Traseul este corect deoarece lungimea drumului $9.66$0 este mai mică decât valoarea dată $L_{max} = 11$