tzigla

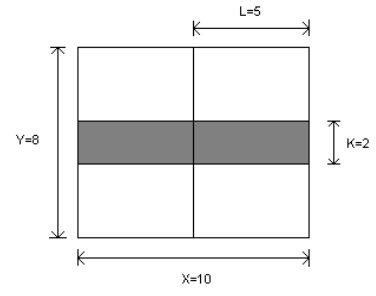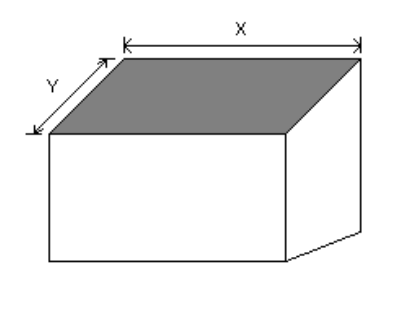
Gigel tocmai şi-a construit o casă de care este foarte mândru. Rămâne totuşi un detaliu de pus la punct: acoperişul. Mai exact, este vorba de o suprafaţă dreptunghiulară de dimensiuni $X$ şi $Y$, numere naturale nenule, unde $X$ este lăţimea dreptunghiului, iar $Y$ este înălţimea acestuia. Suprafaţa trebuie acoperită cu bucăţi pătratice de ţiglă, toate având aceeaşi latură $L$ (număr natural nenul). Ţigla va trebui să acopere întreaga suprafaţă a acoperişului, fără a o depăşi. Bucăţile de ţiglă care se învecinează pe orizontală nu se pot suprapune; în schimb cele care se învecinează pe verticală trebuie să se suprapună pe o suprafaţă dreptunghiulară, aceasta având latura orizontală (lăţimea) egală cu dimensiunea ţiglei $L$ şi latura verticală (înălţimea) egală cu $K$ (număr natural nenul). Având aptitudini de informatician, Gigel observă că pentru nişte valori $X$, $Y$ şi $K$ cunoscute este posibil să existe zero, una sau mai multe valori ale lui $L$, astfel încât suprafaţa să poată fi acoperită în condiţiile enunţate. Gigel plăteşte în funcţie de suprafaţa totală de ţiglă cumpărată. De aceea, el şi-ar dori să aleagă ţiglă de latură $L$ astfel încât costul total să fie cât mai mic.

Cerinţă

Scrieţi un program care calculează latura $L$ a ţiglei folosite. Dacă nu există soluţie, se va afişa valoarea $0$.

Date de intrare

Din fișierul de intrare tzigla.in se citesc $3$ valori, fiecare de pe câte un rând, în următoarea ordine:

• $X = \text{lăţimea zonei care trebuie să fie acoperită}$
• $Y = \text{înălţimea zonei care trebuie să fie acoperită}$
• $K = \text{înălţimea zonei de intersecţie între două ţigle}$

Date de ieşire

Fișierul de ieșire tzigla.out va conține o singură linie pe care se va afișa valoarea

• $L = \text{dimensiunea unei ţigle folosite pentru acoperiş sau} \ 0, \ \text{dacă nu există nici o valoare convenabilă pentru} \ L.$

Restricţii şi precizări

• $1 \leq X \leq 1 \ 000 \ 000$
• $1 \leq Y \leq 1 \ 000 \ 000$
• $1 \leq K \leq X$ şi $1 \leq K \leq Y$
• pentru o valoare corectă a lui $L$, dar care nu este optimă din punct de vedere financiar, se acordă $50\%$ din punctaj.

Exemplul 1

tzigla.in

14
9
3

tzigla.out

0

Explicaţie

Pentru datele de intrare nu există soluţie, deci se afişează $0$.

Exemplul 1

tzigla.in

10
8
2

tzigla.out

5

Explicaţie