paianjen

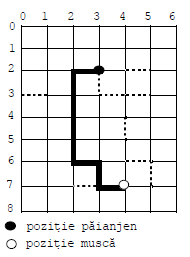
Un păianjen a ţesut o plasă, în care nodurile sunt dispuse sub forma unui caroiaj cu $m$ linii (numerotate de la $0$ la $m-1$) şi $n$ coloane (numerotate de la $0$ la $n-1$) ca în figură. Iniţial, Oricare două noduri vecine (pe orizontală sau verticală) erau unite prin segmente de plasă de lungime $1$. În timp unele porţiuni ale plasei s-au deteriorat, devenind nesigure. Pe plasă, la un moment dat, se găsesc păianjenul şi o muscă, în noduri de coordonate cunoscute.

Cerinţă

Să se determine lungimea celui mai scurt traseu pe care trebuie să-l parcurgă păianjenul, folosind doar porţiunile sigure ale plasei, pentru a ajunge la muscă. De asemenea, se cere un astfel de traseu.

Date de intrare

Fişierul de intrare paianjen.in conţine:

• pe prima linie două numere naturale $m$, $n$, separate printr-un spaţiu, reprezentând numărul de linii şi respectiv numărul de coloane ale plasei;
• pe a doua linie două numere naturale $l_p$, $c_p$, separate printr-un spaţiu, reprezentând linia şi respectiv coloana nodului în care se află iniţial păianjenul;
• pe linia a treia două numere naturale $l_m$, $c_m$ separate printr-un spaţiu, reprezentând linia şi respectiv coloana pe care se află iniţial musca;
• pe linia a patra, un număr natural $k$, reprezentând numărul de porţiuni de plasă deteriorate;
• pe fiecare dintre următoarele $k$ linii, câte patru valori naturale $l_1$, $c_1$, $l_2$, $c_2$, separate prin câte un spaţiu, reprezentând coordonatele capetelor celor $k$ porţiuni de plasă deteriorate (linia şi apoi coloana pentru fiecare capăt).

Date de ieșire

Fişierul de ieşire paianjen.out va conţine pe prima linie un număr natural min reprezentând lungimea drumului minim parcurs de păianjen, exprimat în număr de segmente de lungime $1$. Pe următoarele min+1 linii sunt scrise nodurile prin care trece păianjenul, câte un nod pe o linie. Pentru fiecare nod sunt scrise linia şi coloana pe care se află, separate printr-un spaţiu.

Restricții și precizări

• $1 \leq m, n \leq 140$;
• $1 \leq k \leq 2 \cdot (m \cdot n-m-n+1)$;
• Lungimea drumului minim este cel mult $15 \ 000$
• Pentru datele de test există întotdeauna soluţie. Dacă problema are mai multe soluţii, se va afişa una singură.
• Porţiunile nesigure sunt specificate în fişierul de intrare într-o ordine oarecare. Oricare două porţiuni nesigure orizontale se pot intersecta cel mult într-un capăt. De asemenea, oricare două porţiuni nesigure verticale se pot intersecta cel mult într-un capăt.
• Se acordă $30\%$ din punctaj pentru determinarea lungimii drumului minim şi $100\%$ pentru rezolvarea ambelor cerinţe.

Exemplu

paianjen.in

9 7
2 3
7 4
8
2 4 2 5
2 3 3 3
3 0 3 1
3 3 3 5
4 4 5 4
6 4 6 5
6 5 7 5
7 2 7 3

paianjen.out

8
2 3
2 2
3 2
4 2
5 2
6 2
6 3
7 3
7 4

Explicație

Problema corespunde figurii de mai sus. Traseul optim este desenat cu linie groasă, iar porţiunile nesigure sunt desenate punctat.