rez

Gigel este electronist amator. El afirmă că a inventat o nouă componentă electronică denumită reziston. În mod ciudat totuşi rezistonii au nişte proprietăţi care nouă ne sună foarte cunoscut:

1. Orice reziston este caracterizat printr-o mărime fizică numită rezistonţă. Aceasta poate avea ca valori numai numere naturale.
2. Rezistonii pot fi legaţi între ei în serie sau în paralel, formând astfel circuite.
3. Fie doi rezistoni având rezistonţele $R_1$, respectiv $R_2$. Legarea în serie a rezistonilor se realizează astfel:

Rezistonţa acestui circuit va fi $R_1$ + $R_2$.
4. Legarea celor doi rezistoni în paralel se realizează astfel:

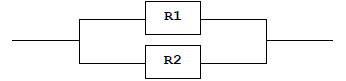
Rezistonţa acestui circuit va fi $\frac{R_1 \cdot R_2}{R_1 + R_2}$. Fiindcă rezistonţele pot fi numai numere naturale, împărţirea este întreagă (adică rezultatul este câtul împărţirii întregi a lui ($R_1 \cdot R_2$) la ($R_1 + R_2$)).
5. Prin legarea oricâtor rezistoni în serie şi în paralel se obţin circuite. Circuitele pot fi legate în serie şi/sau în paralel după aceleaşi reguli. Rezistonţa unui circuit se calculează aplicând regulile de mai sus.

Un circuit va fi codificat printr-un şir de caractere construit după următoarele reguli:

1. Dacă circuitul $C$ este format dintr-un singur reziston şi acesta are rezistonţa de valoare $x$, atunci codificarea circuitului $C$ este $R_x$. Rezistonţa circuitului $C$ va fi $x$.
2. Dacă circuitul $C$ este obţinut prin legarea în serie a două sau mai multe circuite, codificate $C_1$, $C_2$, $\dots$, $C_k$, atunci codificarea circuitului $C$ se obţine concatenând în ordine codificările circuitelor $C_1$, $C_2$, $\dots$, $C_k$. Rezistonţa circuitului $C$ se obţine prin însumarea rezistonţelor circuitelor $C_1$, $C_2$, $\dots$, $C_k$.
3. Dacă circuitul $C$ este obţinut prin legarea în paralel a două sau mai multe circuite, atunci codificarea circuitului $C$ se obţine încadrând între paranteze rotunde codificările circuitelor din care este format şi separând aceste codificări prin virgulă: ($C_1$, $C_2$, $\dots$, $C_k$), $k > 1$. Rezistonţa circuitului $C$ este egală cu câtul împărţirii produsului dintre rezistonţele $C_1$, $C_2$, $\dots$, $C_k$ şi suma rezistonţelor circuitelor $C_1$, $C_2$, $\dots$, $C_k$.

Cerinţă

Scrieţi un program care să determine rezistonţa unui circuit.

Date de intrare

Fişierul de intrare rez.in conţine pe prima linie un şir de caractere care reprezintă codificarea unui circuit conform regulilor de mai sus.

Date de ieşire

Fişierul de ieşire rez.out conţine o singură linie pe care este scrisă rezistonţa circuitului specificat în fişierul de intrare.

Restricții și precizări

• $0$ < lungimea codificării unui circuit $\leq 1 \ 000$
• $0$ < rezistonţa oricărui reziston < $100$
• $0$ < rezistonţa oricărui circuit < $2 \ 000 \ 000 \ 000$ (două miliarde)
• Şirul prin care se codifică un circuit nu conţine spaţii.
• Pentru datele de test nu se vor obţine împărţiri la $0$.

Exemplul 1

rez.in

R12

rez.out

12

Exemplul 2

rez.in

R42R33R3

rez.out

78

Exemplul 3

rez.in

R2(R5,R69,R12)R80

rez.out

130

Exemplul 4

rez.in

(R5,R3(R12,R4),R3)

rez.out

6