Se consideră un arbore (graf conex aciclic) cu N vârfuri, fără rădăcină fixată. Drept rădăcină, poate fi ales oricare dintre vârfuri. Să presupunem că a fost ales vârful cu numărul T. Între oricare vârf şi T există un drum unic care conţine fiecare vârf al arborelui cel mult o singură dată (un drum între vârfurile i şi j este o secvenţă de vârfuri, care începe cu i, se termină cu j, iar între oricare două vârfuri consecutive există o muchie în arbore). Fiecărui vârf i(inclusiv T) trebuie să i se asocieze o valoare , mai mare sau egală cu 0, astfel încât suma valorilor vârfurilor de pe drumul dintre i şi rădăcina T, împărţită la K, să dea restul . Se defineşte costul arborelui cu rădăcina fixată în T, , ca fiind suma valorilor asociate fiecărui nod. Dintre toate posibilităţile de alegere a valorilor care respectă condiţia precizată anterior, se va alege aceea pentru care este minim.
Se constată uşor că alegând alt vârf drept rădăcină, de exemplu, vârful S (diferit de T), nu este neapărat egal cu .
Cerinţă
Dându-se un arbore cu N vârfuri, un număr întreg K şi valorile , corespunzătoare fiecărui vârf, determinaţi acele vârfuri T care pot fi alese drept rădăcină, pentru care costul este minim (adică , oricare ar fi S diferit de T), precum şi costul respectiv.
Date de intrare
Pe prima linie a fişierului de intrare asmin.in se află 2 valori întregi: N şi K. Pe următoarele N-1 linii se află câte două numere întregi a b, separate printr-un spaţiu, având semnificaţia că există muchie între vârfurile a şi b. Vârfurile sunt numerotate de la 1 la N. Pe următoarea linie se află N numere întregi, reprezentând valorile .
Date de ieşire
Pe prima linie a fişierului de ieşire asmin.out se vor afişa două valori întregi: C şi M. C reprezintă costul minim posibil al arborelui. M reprezintă numărul de vârfuri care pot fi alese drept rădăcină şi pentru care se obţine costul C. Pe a doua linie se află M numere întregi separate prin câte un spaţiu, scrise în ordine crescătoare, reprezentând numerele vârfurilor ce pot fi alese ca rădăcină astfel încât să se obţină costul C.
Restricţii şi precizări
2 ≤ N ≤ 16 0002 ≤ K ≤ 1000- Cel puţin
40%din testele folosite la evaluare vor aveaN ≤ 1000
Exemplu
asmin.in
5 3
1 2
1 3
2 4
2 5
0 1 2 1 0
asmin.out
5 2
1 5
Explicații
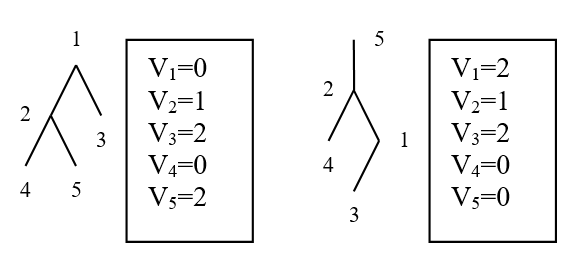
Cei doi arbori obţinuţi (împreună cu valorile asociate vârfurilor) sunt următorii: