Pe planeta Aret există un continent de formă dreptunghiulară împărțit în pătrate identice, dispuse alăturat câte pe fiecare rând și câte pe fiecare coloană. Fiecare pătrat reprezintă câte o țară. Rândurile sunt numerotate de la la de sus în jos, iar coloanele de la la de la stânga la dreapta. O țară situată pe rândul și coloana este identificată prin coordonatele .

Deasupra continentului circulă nori, de diferite tipuri, ca în figura , care sunt formați și ei din pătrate identice, iar suprafața unui pătrat acoperă în întregime suprafața unei țări. Norii pot intra pe continent prin vest și se deplasează pe orizontală spre est, sau pot intra pe continent prin nord și se deplasează pe verticală spre sud.
În fiecare oră, norii se deplasează cu câte o poziție în direcția de deplasare, iar atunci când norul părăsește în totalitate suprafața continentului, intră din nou pe continent deasupra aceleași țări acoperite la prima intrare (poziția inițială) și continuă deplasarea. Norii intră pentru prima dată deasupra continentului după un timp de așteptare W și se pot suprapune în timpul deplasării. Un nor se numește ”întreg”, dacă în timpul deplasării, există cel puțin o oră în care norul este situat deasupra continentului și nu depășește marginile continentului.
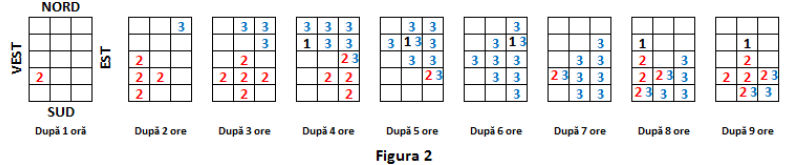
În exemplul din figura sunt trei nori, simbolizați prin cifrele , și . Norul - de tip - pătrunde pe continent prin țara după ore de așteptare, norul - de tip - pătrunde prin țara după ore de așteptare, iar norul - de tip - pătrunde prin țara după oră de așteptare. În acest exemplu este redată poziția fiecărui nor în primele ore. În țările care nu sunt acoperite de nori cerul este senin, iar în țările peste care se suprapun cel puțin doi nori este furtună.
Cerinţe
Cunoscând numerele naturale , , , coordonatele țării pe unde intră fiecare nor pe continent, tipul acestuia, precum și timpul de așteptare al fiecărui nor la prima intrare pe continent, se cere:
- Să se determine numărul al norilor întregi și timpul minim după care toți norii întregi sunt situați deasupra continentului, fără a depăși marginile acestuia;
- Cunoscând și un timp , să se determine numărul de țări care au cerul senin după ore și numărul de țări în care este furtună după ore.
Date de intrare
Fișierul de intrare nori.in conține:
- Pe prima linie, un număr natural care poate avea doar valorile sau ;
- Pe linia a doua, patru numere naturale , , și , în această ordine, despărțite prin câte un spațiu, cu semnificația din enunț;
- Pe următoarele linii se află câte patru numere naturale , , și , unde în această ordine, despărțite prin câte un spațiu. Numerele și reprezintă linia și coloana, țării prin care intră norul pe continent, reprezintă tipul norului , iar reprezintă timpul de așteptare al norului la prima intrare deasupra continentului.
Date de ieșire
- Dacă valoarea lui este , se va rezolva numai cerința ) În acest caz, fișierul de ieșire
nori.outva conține pe prima linie două numere naturale și , în această ordine, despărțite prin câte un spațiu. Numărul reprezintă numărul norilor întregi, iar este timpul minim determinat; - Dacă valoarea lui este , se va rezolva numai cerința ). În acest caz, fișierul de ieșire
nori.outva conține pe prima linie două numere naturale și , în această ordine, despărțite printr-un spațiu. Numărul reprezintă numărul de țări care au cer senin după ore, iar reprezintă numărul de țări în care este furtună după ore.
Restricții și precizări
- ;
- ;
- ;
- ; este număr impar; poate fi mai mare decât sau ;
- ;
- Pentru cerinta ), se garantează că ;
- Pot exista mai mulți nori care intră pe continent prin aceeași țară;
- Niciun nor nu intră pe continent prin țara cu coordonatele ;
- Dacă = atunci
- Dacă = atunci
- Pentru rezolvarea corectă a cerinței . se obține din punctaj, iar pentru cerința . se obține din punctaj.
Exemplul 1
nori.in
1
5 3 3 9
2 1 1 3
4 1 3 0
1 3 5 1
nori.out
2 9
Explicație
Vezi exemplul din figura . Sunt nori întregi și anume norul și norul . Cei doi nori sunt situați în întregime deasupra continentului, prima dată după ore.
Exemplul 2
nori.in
2
5 3 3 9
2 1 1 3
4 1 3 0
1 3 5 1
nori.out
8 2
Explicație
Vezi exemplul din figura . După ore țările cu cer senin sunt la coordonatele:
, , , , , , , iar țările în care este furtună sunt la coordonatele: și .