npath

Fie $N$ și $K$ două numere naturale.

• Toate punctele din plan de coordonate întregi $(x,y)$ cu proprietatea $0 \leq x \leq N, 0 \leq y \leq N$ se unesc prin linii orizontale și verticale de lungime $1$.
• Apoi $K$ linii de lungime $1$ dintre cele de mai sus se șterg.

Definim o cale ca fiind o succesiune continuă de linii orizontale sau verticale de lungime $1$, între originea sistemului de axe și punctul de coordonate $(N, N)$, cu lungimea totală $2 \cdot N$.

Cerință

Să se determine numărul total de căi distincte.

De exemplu, dacă $N = 3$ și dintre toate liniile desenate se șterg $K = 4$ linii (liniile subțiri), atunci conform figurilor de mai jos, numărul total de căi distincte va fi $6$.

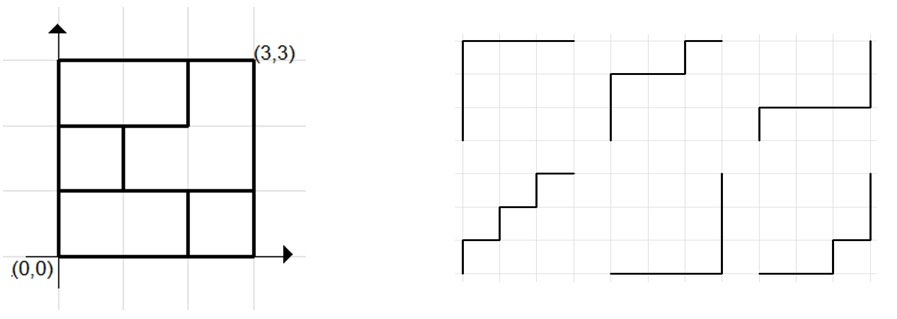
Date de intrare

Fișierul de intrare npath.in conține pe prima linie numerele $N$ și $K$, despărțite printr-un spațiu, cu semnificaţia de mai sus, iar pe fiecare din următoarele $K$ linii va fi câte un triplet de numere $x, y, d$ având următoarea semnificație:

• $x, y$ reprezintă coordonatele punctului de unde începe să se șteargă o linie.
• $d = 1$ dacă linia va fi ștearsă pe orizontală către dreapta.
• $d = 2$ dacă linia va fi ștearsă pe verticală în sus.

Date de ieșire

Fișierul de ieșire npath.out va conține pe prima linie restul împărțirii numărului total de căi distincte la $3000017$.

Restricții și precizări

• $1 \leq N \leq 5 \ 000$
• $0 \leq K \leq 100$
• Două căi sunt distincte dacă succesiunea de linii orizontale și verticale diferă prin cel puțin o poziție
• Pentru teste în valoare de $52$ puncte $0 \leq K \leq 15$

Exemplu

npath.in

3 4
1 0 2
2 1 2
2 2 1
1 2 2

npath.out

6

Explicație

$N = 3$ și $K = 4$. Din grila inițială se șterg $4$ linii și anume:

• Linia verticală dintre punctele de coordonate $(1,0)$ și $(1,1)$
• Linia verticală dintre punctele de coordonate $(2,1)$ și $(2,2)$
• Linia orizontală dintre punctele de coordonate $(2,2)$ și $(3,2)$
• Linia verticală dintre punctele de coordonate $(1,2)$ și $(1,3)$

În total sunt $6$ moduri diferite de a ajunge din origine în punctul de coordonate $(3,3)$ fără a trece prin liniile șterse (conform figurilor de mai sus). Restul împărțirii lui $6$ la $3000017$ este $6$.