expandmat

Fie o matrice $A$ de dimensiuni $2^N$ x $2^N$ date. Aceasta se construiește astfel:
Se pornește de la o matrice de dimensiune $2$ x $2$ având ca elemente litere mici ale alfabetului englez. Matricea $B$ de dimensiune $2^k$ x $2^k$ se formează din patru submatrice de dimensiune $2^{k-1}$ x $2^{k-1}$ și se obține din matricea $C$ de dimensiune $2^{k-1}$ x $2^{k-1}$, astfel:

• Submatricea din stânga sus va fi $C$
• Submatricea din dreapta sus va fi formată din $C$, crescând fiecare element cu $3$ (a devine d, b devine e, z devine c)
• Submatricea din stânga jos va fi formată din $C$, scăzând fiecare element cu $4$ (a devine v, b devine x, \dots, z devine u)
• Submatricea din dreapta jos este $C$ rotită cu $180$ de grade
• De exemplu dacă $C$ de dimensiune $2$ x $2$ are valoarea:

De exemplu dacă $C$ de dimensiune $2$ x $2$ are valoarea:

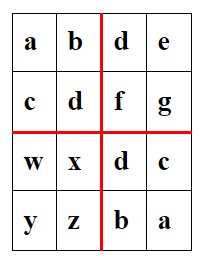
Atunci matricea $B$ de dimensiune $2^2$ x $2^2$ are valoarea:

Cerința

Se dau $Q$ triplete $(i, j, L)$, cu semnificația: pe poziția $A{i,j}$ se află litera $L$. Care este numărul maxim de triplete care se pot selecta astfel încât toate să fie adevărate?

Exemplu:
$N = 2, Q = 7$
(1, 2, b)
(2, 3, f)
(2, 1, d)
(1, 2, z)
(4, 1, y)
(4, 4, a)
(3, 3, d)

Răspunsul este $5$ (prima, a doua și ultimele trei). De exemplu, dacă matricea de pornire este:

• $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$

Atunci matricea $A$ va fi:

• $\begin{pmatrix} a & b & d & e \\ c & d & f & g \\ v & x & d & c \\ y & z & b & a \end{pmatrix}$

Date de intrare

Fișierul de intrare expandmat.in conține pe prima linie numerele $N$ și $Q$, despărțite printr-un spațiu, cu semnificaţia de mai sus, iar pe fiecare din următoarele $Q$ linii va fi câte un triplet de numere $i, j, L$ cu semnificațiile din enunț.

Date de ieșire

Fișierul de ieșire expandmat.out va conține pe prima linie numărul maxim de triplete care se pot selecta astfel încât toate să fie adevărate.

Restricții și precizări

• $1 \leq N \leq 60$
• $1 \leq Q \leq 100 \ 000$
• Matricea este indexată de la $1$.

Exemplul 1

expandmat.in

2 7
1 2 b
2 3 f
2 1 d
1 2 z
4 1 y
4 4 a
3 3 d

expandmat.out

5

Explicație

N = 2 și Q = 7.
Cele $5$ triplete care se pot alege sunt:
(1, 2, b)
(2, 3, f)
(4, 1, y)
(4, 4, a)
(3, 3, d)

Dacă matricea inițială este:

• $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$

Atunci matricea finală este:

• $\begin{pmatrix} a & b & d & e \\ c & d & f & g \\ v & x & d & c \\ y & z & b & a \end{pmatrix}$

Această matrice satisface toate cele $5$ triplete.