Multiselect

William has recently been working on select algorithms! In case you’re not already familiar with them, these algorithms receive an array of length $M$ and an index $K \leq M - 1$ in input. Then, through $M$ steps they rearrange the array contents, so that the $K$-th element is in position $K$ of the array, with all smaller elements sitting on its left side, and all larger elements on its right side. No relative order, however, can be assumed between elements within a same side.

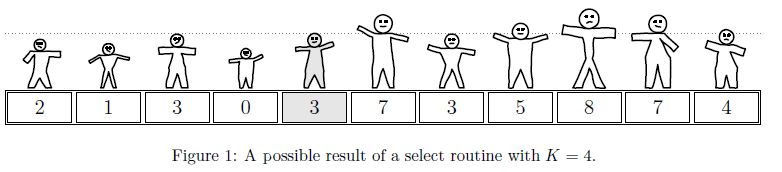
The select algorithm is ready, however, the problem William has to tackle requires a bit more work. He needs to process a very large array of length $M$, so that at the end $N$ given different indexes $K_0$, $\dots$, $K_{N-1}$ are all partitioning the array.

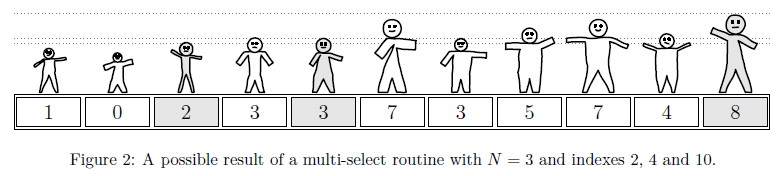
Since William is lazy, he doesn’t want to write a new algorithm from scratch! Instead, he plans to re-use the select algorithm multiple times to achieve the desired effect. For example, assume that $M = 11$, $N = 3$ and the indexes $K_i$ are $2$, $4$, $10$, as in Figure $2$. One possible way to achieve the effect could be:

• first, run select on the whole vector with $K = 4$ (as in Figure $1$), spending $11$ algorithm steps;
• then, run select on the sub-vector [$0 \dots 3$] with $K = 2$, which requires $4$ algorithm steps;
• finally, run select on the sub-vector [$5 \dots 10$] with $K = 10$, which requires $6$ algorithm steps.

Overall, the procedure will require $11$ + $4$ + $6$ = $21$ algorithm steps. Notice that this is not the only possible way to obtain the result! Another could be:

• run select on the whole vector with $K = 10$, spending $11$ steps;
• run select on the sub-vector [$0 \dots 9$] with $K = 2$, spending $10$ steps;
• run select on the sub-vector [$2 \dots 9$] with $K = 4$, spending $8$ steps.

With this other strategy, the procedure will require $11$ + $10$ + $8$ = $29$ steps $\dots$ not so good! Help William perform his task, minimising the number of algorithm steps required.

Input data

The first line contains the two integers $N$ and $M$. The second line contains $N$ integers $K_i$.

Output data

You need to write a single line with an integer: the minimum total number of algorithm steps required to multi-select the given indexes from an array of length $M$.

Constraints and clarifications

• $1 \leq N \leq 1 \ 000$;
• $1 \leq M \leq 10^8$;
• $0 \leq K_0 < K_1 < \dots < K_{N-1} < M$;

Example 1

stdin

3 11
2 4 10

stdout

21

Explanation

The first sample case is the one described in the problem statement.

Example 2

stdin

3 101
49 50 51

stdout

152

Explanation

In the second sample case, one way of achieving the lowest amount of steps is to first select $K_0$ = $49$ in $101$ steps, then $K_2$ = $51$ in further $51$ steps, getting $K_1$ = $50$ in place for free.