Giorgio’s high-school in Italy is serious about the IIOT: all its the students are training for the next edition of the contest, and they absolutely want to earn their school a medal. The head Computer Science professor of the school has prepared a detailed training program for his students: a map of all the tasks that should be fully solved in order to be ready for the competition.

The map is given as a rooted tree with nodes (numbered from to ) where each node represents a task, and the parent-child relationships represent restrictions in the order in which the tasks should be solved. More specifically: if a task has a task among its children, this means that the task should be solved first in order to “unlock” the task .
The students know, for each task , the time (in hours) that it would take a single student to solve the task with no external help. Because of how the map is made, these tasks can be attempted in parallel: multiple tasks can be attempted at the same time by different students, however it’s not possible for multiple students to work on the same task.
Help the students calculate the minimum amount of hours that it will take them to solve all the tasks in the map. But wait! To make things more interesting, the professor agreed that the students can “cheat” a maximum of times: this means that for tasks they will be able to simply find a solution online, spending hours on those tasks.
Input data
The first line contains two integers and , the total number of tasks in the map and the number of tasks that students are allowed to solve by “cheating”. The next lines describe the tasks: the -th line (with going from to ) contains two integers and , which indicate that:
- Before solving task , a student must solve task . If = , then task is the root of the map and it’s the first task to solve.
- Solving task without any help will take a student hours.
Output data
You need to write a single integer: the minimum number of hours that the students will need to solve all the tasks.
Constraints and clarifications
- .
- .
- for each .
- for exactly one value of , and for all other values of .
- Following the chain always leads to the root of the tree, for each .
- The school has enough students to tackle as many tasks in parallel as needed.
| # | Score | Constraints |
|---|---|---|
| 1 | 0 | Examples |
| 2 | 18 | |
| 3 | 9 | |
| 4 | 23 | |
| 5 | 29 | |
| 6 | 21 | No additional limitations. |
Example 1
stdin
5 2
3 10
4 1
3 5
-1 20
3 2
stdout
5
Explanation
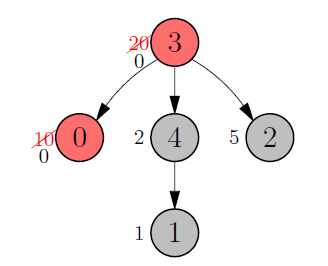
The first sample case is shown on the right: there are tasks and only of them can be skipped. Skipping task and task leads to the optimal solution, whose total time is hours. After skipping task (the root), task and can be tackled in parallel; after hours task is solved and task can be started.
After hours, task is solved and you cannot choose another set of tasks to skip to reduce this time.
Example 2
stdin
7 2
1 10
-1 1
3 10
1 3
1 7
0 7
5 9
stdout
14
Explanation
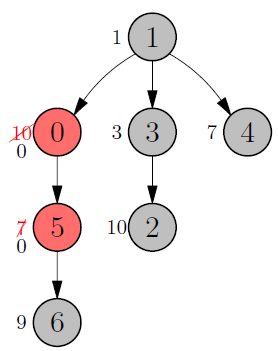
The second sample case has tasks and only of them can be skipped. A possible optimal solution is shown on the right, reducing the total time down to hours.