You have a rectangular sheet of paper with dimensions $N \times M$ centimeters. The sheet is squared into a net of squares $1 \times 1$ centimeters each. You can consider the sheet as a coordinate system — its lower left corner is the origin $(0,0)$ of the coordinate system and each vertex of a square is assigned with integer coordinates — between $0$ and $N$ on the $x$ axis and between $0$ and $M$ on the $y$ axis. You are receiving a sequence of requests for cutting the sheet of paper (or more precisely, the piece that has left from it). Each request is defined by a pair of nonnegative integers $(p, q)$, representing a vertex from the net, that is situated into the uncut portion of the paper. Cutting is executed according to the following algorithm: two segments are drawn, both starting at point $(p,q)$, one is at an angle of $45 \degree$, and the other at an angle of $135 \degree$ to the axis $x$, pointed "upwards", i.e. with increasing $y$. Both segments end at the border of the rectangular sheet of paper. After that the portion of the paper that is above the drawn segments is cut off and the rest piece of paper remains as a new figure (see the example pictures)

Following is an example with starting rectangular paper with dimensions $N=20$ and $M=10$, as well as all figures that remain after following cutting requests:

• $(10,5)$ — the blue part is cut
• $(4,7)$ — the red part is cut
• $(0,1)$ — the green part is cut
• $(16,3)$ — the brown part is cut
  
  

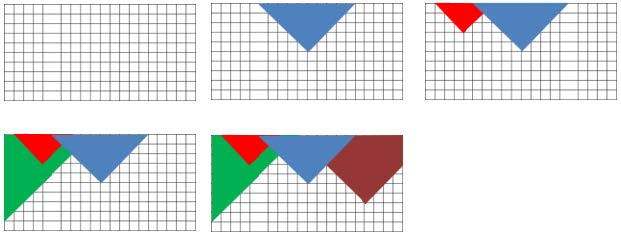
Task

Write a program that after each request calculates the remaining figure's area.

Important: It is possible to receive a request which will define one of the segments with length $0$, for example if the point is situated on the leftmost or rightmost border of the rectangle. However, it is guaranteed that each request will lead to cutting a positive area figure.

Input

From the first line of the standard input read two positive integers $N$ and $M$ — dimensions of the initial sheet of paper. From the second line read a positive integer $Q$ — number of cutting requests. From the last $Q$ lines read two nonnegative integers $x$ and $y$, separated by space — coordinates of the point, which defines a cutting request.

Output

For each cutting request, on a seperate line, your program should print one number — area of the paper figure remaining after the cutting. The value of the area should be printed with two digits after the decimal point.

Constraints

• $1 ≤ N \cdot M ≤ 10^{12}$
• $1 ≤ Q ≤ 150 \ 000$
• In $20 \%$ of the tests: $1 ≤ N ≤ 10 \ 000, 1 ≤ Q ≤ 10 \ 000$
• In $52 \%$ of the tests: $1 ≤ N ≤ 1 \ 000 \ 000$
• Each test is evaluated separately.

Example

stdin

20 10
4    
10 5 
4 7  
0 1  
16 3 

stdout

175.00
167.00
138.50
103.00

Explanation

The example corresponds to the example with pictures above.