Hai sa facem si noi ceva #5 | Hurry Up | 2sah

Se dă o tablă de șah cu n + 1 linii (numerotate de sus în jos începând cu 1) și 2n + 1 coloane (numerotate de la stânga la dreapta începând cu 1). Pe prima linie pătratul din mijloc conține 1 gram de fân, iar celelalte pătrate de pe prima linie nu conțin nimic. Începând cu linia a doua fiecare pătrat conține o cantitate de fân obținută prin adunarea cantităților de fân din cele 3 pătrate ale liniei anterioare cu care se învecinează (pe verticală și diagonală). De exemplu dacă n = 3 tabla are 4 linii, 7 coloane și următoarea configurație.



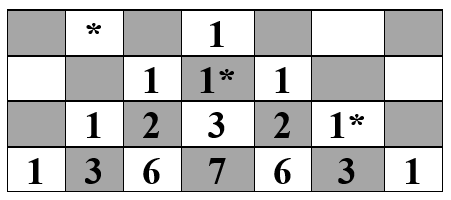
Un cal pleacă de pe prima linie, de pe o coloana k ≤ n, sare din orice poziție (i, j) în poziția (i + 1, j + 2) atât timp cât este posibil și mănâncă tot fânul din pătratele prin care trece. De exemplu, pentru n = 3 și k = 2, pătratele prin care trece calul sunt marcate cu asterisc ( * )

Cerinţe

1. Cunoscând n și k, să se calculeze cantitatea de fân de pe linia k a tablei.
2. Cunoscând n și k, să se calculeze câte grame de fân mănâncă un cal care pleacă de pe prima linie, de pe coloana k.

Întrucât aceste numere pot fi mari, se cere doar restul modulo 100003 ale acestor numere.

Date de intrare

Fișierul de intrare 2sah.in va conține pe prima linie un număr t cu valoarea 1 sau 2. Pe a doua linie a fișierului de intrare se găsesc două numere naturale n și k separate printr-un spațiu.

Dacă t = 1 se va rezolva prima cerință, deci pentru valoarea n citită tabla are n + 1 linii și 2n + 1 coloane, iar k reprezintă numărul liniei de pe care trebuie calculată cantitatea de fân.

Dacă t = 2 se va rezolva a doua cerință, deci pentru valoarea n citită tabla are n + 1 linii și 2n + 1 coloane, iar k reprezintă numărul coloanei din prima linie de unde pleacă calul.

Date de ieşire

Dacă t din fișierul de intrare este 1 se va rezolva doar prima cerință.
În acest caz fișierul de ieșire 2sah.out va conține un singur număr reprezentând cantitatea totală de fân din toate pătratele situate pe tabla pe linia k (trebuie afișat restul modulo 100003).

Dacă t din fișierul de intrare este 2 se va rezolva doar a doua cerință.
În acest caz fișierul de ieșire 2sah.out va conține un singur număr reprezentând cantitatea totală de fân mâncată de un cal care pleacă de pe linia 1 și coloana k (trebuie afișat restul modulo 100003).

Restricții și precizări

• $1 \le k \le n \le 1\ 000\ 000\ 000$
• La cerința 1 pentru $80\%$ dintre teste $k \le n \le 1\ 000\ 000$, iar pentru alte $20\%$ din teste $k \le n \le 1\ 000\ 000\ 000$.
• La cerința 2 pentru $30\%$ dintre teste $k \le n \le 1\ 000$, pentru alte $30\%$ dintre teste $k \le n \le 1\ 000\ 000$, iar pentru restul de $40\%$ dintre teste $k \le n \le 1\ 000\ 000\ 000$.
• Rezolvarea corectă a primei cerințe asigură $20\%$ din punctajul testului respectiv.
• Rezolvarea corectă a celei de a doua cerințe asigura $80\%$ din punctajul testului respectiv.

Exemple

2sah.in

1
3 2

2sah.out

3

2sah.in

2
3 2

2sah.out

2

Explicații

Pentru primul test:
t = 1, deci se rezolvă prima cerință.
Pe linia a doua există 3 pătrate care conțin fiecare câte un gram de fân.(vezi desenul din enunț)

Pentru al doilea test:
t = 2, deci se rezolvă doar a doua cerință.
Traseul calului este: (1, 2) → (2, 4) → (3, 6) adică exact pătrățelele marcate cu asterisc în desenul din enunț. Prima poziție nu conține fân, iar celelalte două conțin câte un gram de fân. Deci calul mănâncă 2 grame de fân.