Mirror IIOT 2023-2024 Round I | Long Chain

You are given a tree with $N$ vertices, numbered from $1$ to $N$ (a tree is an undirected connected graph in which there are no cycles).
You are asked to partition it into edge-disjoint simple paths such that the length of the shortest one is maximized.

In this task, the length of a path is defined as the number of edges it has.

Input data

The first line contains an integer $N$. The next $N - 1$ lines contain $2$ integers $u_i, v_i$, denoting an edge of the tree.

Output data

You need to write a single line with an integer: the maximum length of the shortest path over all partitions of the tree into edge-disjoint simple paths.

Constraints and clarifications

• $2 \leq N \leq 100 \ 000$.
• $1 \leq u_i, v_i \leq N$.
• For tests worth $10$ points, $N \leq 8$.
• For tests worth $20$ more points, $N \le 100$.
• For tests worth $20$ more points, $N \le 1000$.

Example 1

stdin

9
9 8
7 4
7 8
2 1
6 3
5 1
5 8
3 8

stdout

4

Explanation

In the first sample case, an optimal split would be into $2$ edge-disjoint paths, each of length $4$: $2-1-5-8-9$ and $4-7-8-3-6$.

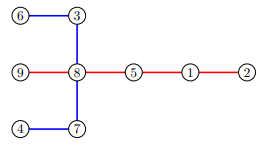
Example 2

stdin

5
1 2
2 3
3 4
2 5

stdout

2

Explanation

In the second sample case, an optimal split would be into $2$ edge-disjoint paths, each of length $2$: $1-2-5$ and $2-3-4$.

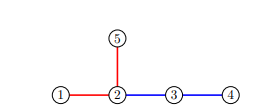
Example 3

stdin

10
7 6
9 6
8 5
4 2
1 3
5 6
1 10
7 10
2 6

stdout

4

Explanation

In the third sample case, an optimal split would be into $2$ edge-disjoint paths, one of length $4$: $4-2-6-5-8$ and the other one of length $5$: $3-1-10-7-6-9$.

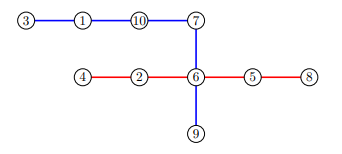
Example 4

stdin

6
1 2
2 3
3 4
4 5
5 6

stdout

5

Explanation

In the fourth sample case, the whole tree consists of only one path of length $5$.