The Earth can be viewed as a matrix with rows and columns, consisting only of the digits and , where represents an island and represents water. After extensive research, it has been discovered that each island needs at least neighboring water positions to transform and become water. The neighbors of an island can be in the N, S, E, or W directions. Additionally, islands have a single special direction (NE, SE, SW, or NW) which represents another neighbor for that island. The transformation of an island into water takes one year.
Task
Knowing the islands, the number for each island, and each special direction:
- Determine how many islands transform into water after one year.
- For queries of the form , determine after how many years the island located at will become water. If it is not possible for to become water, print
-1.
Input data
The first line of the input contains natural numbers, , , , and , in this order, separated by a space. The next lines each contain four natural numbers , , , and , separated by a space, representing the coordinates of an island, the number of neighboring water positions required for it to transform, and its special direction. For , the direction is NE, for , SE, for , SW, and for , NW. If , then on the next line, the number of queries is read, and on the following lines, the numbers and , separated by a space, are read.
Output data
If , then print the number of islands that transform into water after one year. If , then print the answer to each of the queries, each on a separate line.
Constraints and clarifications
- There is a chance that some neighbors are outside the Earth. These will not be considered. For example, an island at position with cannot become water because the northern neighbor does not exist.
- It is guaranteed that for each of the queries, represents a position where an island is located.
- The coordinate represents the row of the matrix, and the coordinate represents the column of the matrix.
- In coordinates where there is no island, there is water.
- To solve this problem in C++, researchers recommend using the following lines of code at the beginning of the
main()function:
ios::sync_with_stdio(0);
cin.tie(0);
| # | Points | Constraints |
|---|---|---|
| 1 | 21 | |
| 2 | 23 | , |
| 3 | 56 | No additional constraints |
Example 1
stdin
1 4 5 9
1 1 1 2
1 2 2 3
1 5 2 1
2 2 4 3
3 4 2 1
4 2 3 1
4 3 2 2
4 4 4 4
4 5 0 1
stdout
7
Example 2
stdin
2 4 5 9
1 1 1 2
1 2 2 3
1 5 2 1
2 2 4 3
3 4 2 1
4 2 3 1
4 3 2 2
4 4 4 4
4 5 0 1
5
1 1
1 5
2 2
4 3
4 4
stdout
1
1
1
2
3
Explanation
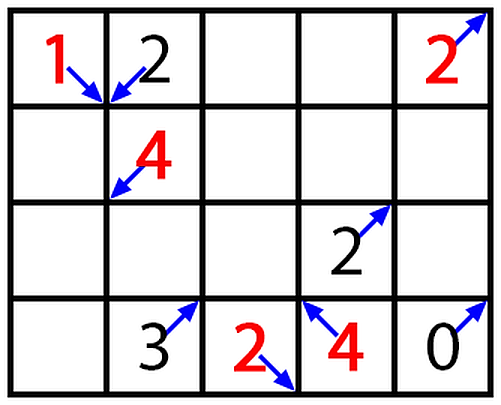
The image below corresponds to both examples. The numbers on an island represent the value of the island, the arrows represent the special direction of the island, and if the value of the island is in red, it means that island is a query from the queries.
Let's discuss the island at position . It has , so it must have at least 2 water neighbors to transform into water. The special direction of this island is NE (northeast). Thus, its water neighbors are in the N, NE, E, and W directions. Since , this island will transform into water.
The islands that transform into water after the first year are: .