Time limit: 2s
Memory limit: 128MB
Input:
Given , , , and a directed acyclic graph (DAG) consisting of nodes (numbered from to ) and edges. Find the lexicographically smallest path that ends at node .
A sequence is lexicographically smaller than sequence if and only if:
- and , , or
- There exists a position such that and , , , , and .
Input data
The first line contains three natural numbers, , , and , representing the number of nodes, the number of edges, and the node where the path will end. The next lines contain two numbers each, and , indicating that there is an edge from node to node .
Output data
The first line contains the number , representing the length of the lexicographically smallest path. The second line contains a sequence of length , representing the lexicographically smallest path.
Constraints and clarifications
- , for each edge
Example 1
stdin
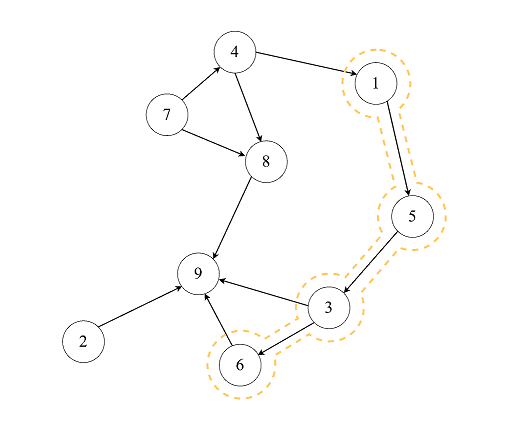
9 11 6
4 1
6 9
5 3
3 9
1 5
3 6
2 9
8 9
4 8
7 8
7 4
stdout
4
1 5 3 6