Task
Consider a network of radios, linked together by communication channels. We model the radios and the communication channels as a tree. Each radio can be in one of three states: without signal (NS), with signal (S), or deactivated (D). Once a radio is in state S or D, it stays in that state permanently - on the other hand a radio in state NS can still change state.
Every day the following occurs simultaneously: every radio in state S will attempt to transmit to every other radio to which it is directly linked by a communication channel. Consider any radio in state NS, and suppose it received transmissions today. If , then remains in state NS tomorrow. If , then enters state S permanently starting tomorrow. If , then enters state D permanently starting tomorrow.
Note that no matter the current state of the network, there will eventually be a day from which no radio ever changes state again. Call this final state of the network the stable state.
Little Steve has queries of the form:
Suppose radios are initially in state
S, and all other radios are in stateNS. How many radios will be in stateSwhen the network reaches its stable state?
Can you answer Little Steve's queries?
Input data
The first line of the input contains . The next lines contain pairs , which denote the communication channels between the radios. The next line contains . The next lines encode the queries. Each line contains followed by .
Output data
Output the answers to the queries, each on a different line.
Constraints and clarifications
- Each query is independent.
- ;
- ;
- Let denote the sum of over all queries in the input.
- .
| # | Points | Restrictions |
|---|---|---|
| 1 | 2 | |
| 2 | 12 | , |
| 3 | 6 | Radio and radio are always linked, |
| 4 | 11 | At most one radio is linked to three or more other radios. |
| 5 | 19 | |
| 6 | 13 | |
| 7 | 18 | |
| 8 | 19 | No further restrictions. |
Example 1
stdin
6
1 2
1 3
1 4
2 5
1 6
5
3 5 4 6
5 6 3 4 1 5
3 3 5 1
4 3 6 2 1
2 4 6
stdout
4
5
5
6
2
Explanation
In the following drawing, an uncoloured vertex is in state NS, a vertex is in state S and a vertex is in state D.
The tree in this example is
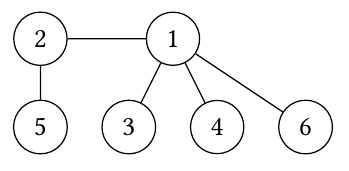
First query. In this case, the tree undergoes the following sequence of states:
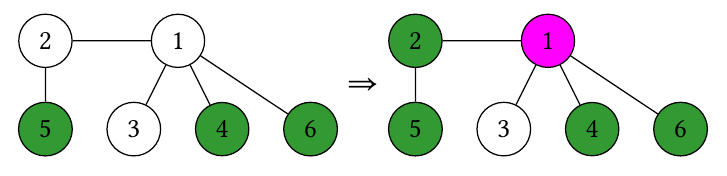
So the answer is , due to vertices .
Second query. The tree undergoes the following sequence of states:
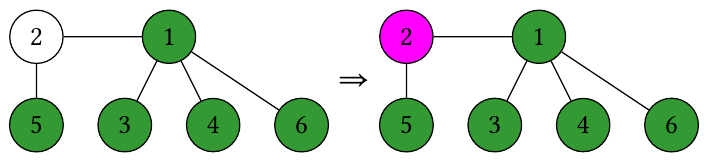
So the answer is , due to vertices .
Third query. The tree undergoes the following sequence of states:
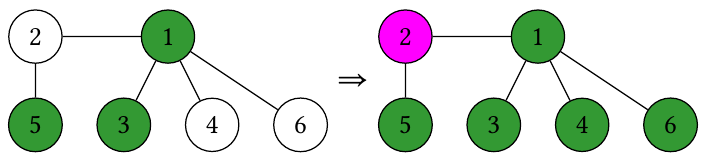
So the answer is , due to vertices .
Fourth query. The tree undergoes the following sequence of states:
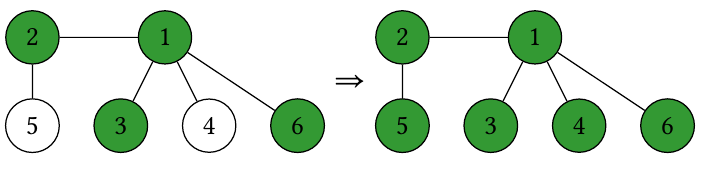
So the answer is , due to vertices .
Fifth query. The tree undergoes the following sequence of states:
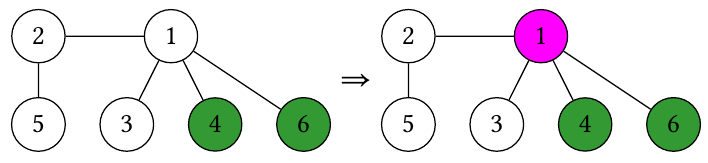
So the answer is , due to vertices .
Example 2
stdin
7
1 2
2 3
3 4
4 5
5 6
6 7
3
3 1 2 5
4 7 6 1 5
5 1 2 3 5 6
stdout
7
6
6
Explanation
The tree in this example is

First query. The tree undergoes the following sequence of states:

So the answer is , due to vertices .
Second query. The tree undergoes the following sequence of states:

So the answer is , due to vertices .
Third query. The tree undergoes the following sequence of states:

So the answer is , due to vertices .
Example 3
stdin
15
1 2
2 3
2 4
2 5
1 6
3 7
2 8
2 9
3 10
3 11
11 12
10 13
13 14
13 15
15
13 3 6 9 2 11 8 5 14 13 15 10 4 1
10 8 9 5 11 2 10 6 12 15 4
11 6 13 4 12 9 11 7 2 3 15 5
11 14 2 15 6 7 12 9 8 3 10 4
2 4 5
10 2 5 7 10 8 15 9 1 14 3
6 14 1 12 15 10 2
3 3 11 15
10 15 3 8 4 6 5 2 11 14 9
4 5 9 4 7
11 12 5 2 3 14 8 7 4 6 1 11
12 8 13 11 3 4 9 7 1 10 2 12 14
4 10 9 6 5
8 7 1 8 5 12 10 15 4
5 11 3 14 10 6
stdout
15
10
13
12
2
14
12
15
13
11
15
15
12
10
13