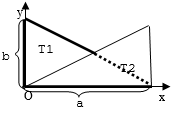
Ionică a primit de ziua lui de la tatăl său un joc format din piese de formă de triunghiulară de dimensiuni diferite şi o suprafaţă magnetică pe care acestea pot fi aşezate. Pe suprafaţa magnetică este desenat un triunghi dreptunghic cu lungimile catetelor , respectiv şi un sistem de coordonate cu originea în unghiul drept al triunghiului, semiaxa pe cateta de lungime , respectiv semiaxa pe cateta de lungime . La un moment dat Ionică aşează pe tabla magnetică piese, pentru care se cunosc coordonatele vârfurilor lor. Tatăl lui Ionică vrea să verifice dacă pe tablă piesele realizează o partiţie a triunghiului dreptunghic desenat, adică dacă sunt îndeplinite condiţiile:
- nu există piese suprapuse;
- piesele acoperă toată porţiunea desenată (în formă de triunghi dreptunghic);
- nu există porţiuni din piese în afara triunghiului desenat.
Cerinţă
Se cere să se verifice dacă piesele plasate pe tabla magnetică formează o partiţie a triunghiului desenat pe tabla magnetică.
Date de intrare
Fişierul de intrare part.in conţine pe prima linie un număr natural , reprezentând numărul de seturi de date din fişier. Urmează grupe de linii, câte o grupă pentru fiecare set de date. Grupa de linii corespunzătoare unui set este formată dintr-o linie cu numerele , , separate între ele prin câte un spaţiu şi linii cu câte şase numere întregi separate prin spaţii reprezentând coordonatele vârfurilor (abscisă ordonată) celor piese, câte o piesă pe o linie.
Date de ieșire
În fişierul part.out se vor scrie linii, câte o linie pentru fiecare set de date. Pe linia () se va scrie dacă triunghiurile din setul de date formează o partiţie a triunghiului desenat pe tabla magnetică sau în caz contrar.
Restricții și precizări
- , sunt numere întregi din intervalul
- Coordonatele vârfurilor pieselor sunt numere întregi din intervalul .
Exemplu
part.in
2
20 10 4
0 5 0 10 10 5
0 0 10 5 0 5
0 0 10 0 10 5
10 0 20 0 10 5
20 10 2
0 0 0 10 10 5
0 0 20 0 20 10
part.out
1
0
Explicație
Figura pentru setul de date

Figura pentru setul de date