Cu toții știm ce este acela un ciur (adică o sită); putem folosi unul pentru a separa făina grunjoasă de cea fină. Cu toate acestea, în problema de față vom încerca să ciuruim nodurile unui arbore.
Nadgob Ciuruitorul are un arbore (graf neorientat conex aciclic) cu noduri. Nadgob vrea să aleagă o submulțime de noduri ale arborelui. Pentru a realiza această alegere, el se va așeza, pe rând, în noduri distincte ale arborelui. Odată așezat într-un nod al arborelui, el poate, de oricâte ori dorește, să selecteze un nod și să "ciuruiască" (adică să adauge la ) toate nodurile pentru care se află pe cel mai scurt drum dintre și . Desigur, un nod care este deja în nu va fi adăugat din nou.
Nadgob se află acum într-o poziție de nelămurire existențială. Plin de angoasă, el se întreabă în câte moduri poate alege submulțimea conform procedurii enunțate anterior (modulo ). Două moduri sunt considerate distincte dacă submulțimile rezultate sunt distincte.
Protocol de interacțiune
Concurentul va implementa funcția solve, cu următoarea semnătură:
int solve (int N, std::vector<int> p, std::vector<int> q, std::vector<int> r);
Parametrii acestei funcții au următoarea semnificație::
- - numarul de noduri ale arborelui;
- - vectori de lungime ce conțin capetele muchiilor arborelui (mai exact, există o muchie bidirecțională între nodurile și , oricare ar fi );
- - vector de lungime ce conține nodurile în care se va așeaza Nadgob, in ordine.
Funcția va întoarce rezultatul cerut în enuntul problemei. Concurentul NU va implementa o funcție main.
Restricții
Subtask 1 (4 puncte)
Subtask 2 (7 puncte)
Subtask 3 (5 puncte)
- Arborele conține cel mult un nod de grad mai mare de .
Subtask 4 (6 puncte)
- Arborele nu conține niciun nod de grad mai mare de .
Subtask 5 (7 puncte)
Subtask 6 (7 puncte)
Subtask 7 (20 puncte)
Subtask 8 (21 puncte)
Subtask 9 (23 puncte)
- Restricții inițiale.
Exemple
Input
3 1
0 1
0 2
0
Output
5
Input
7 4
0 1
0 2
3 0
4 2
3 6
3 5
4 3 1 2
Output
39
Explicații
Pentru primul exemplu:
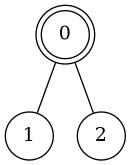
Nadgob se așează în nodul .
- Selectând niciun , rezultă .
- Selectând , rezultă .
- Selectând , rezultă .
- Selectând , rezultă .
- Selectând și , rezultă $S = {1, 2}.
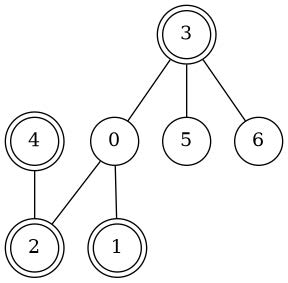
Pentru al doilea exemplu: