cifru

Marele erou Ben10 se află din nou în postura de a salva lumea. De data aceasta el trebuie să dezamorseze o bombă de mare putere, a cărei explozie ar putea distruge omenirea. Dificultatea sarcinii constă în faptul că bomba este protejată printr-un dispozitiv complicat, cu cifru, compus din $N \times N$ butoane aşezate sub forma unui tablou cu $N$ linii şi $N$ coloane, fiecare buton având înscris un număr natural, aşa cum se vede în $\text{Figura} \ 1$.

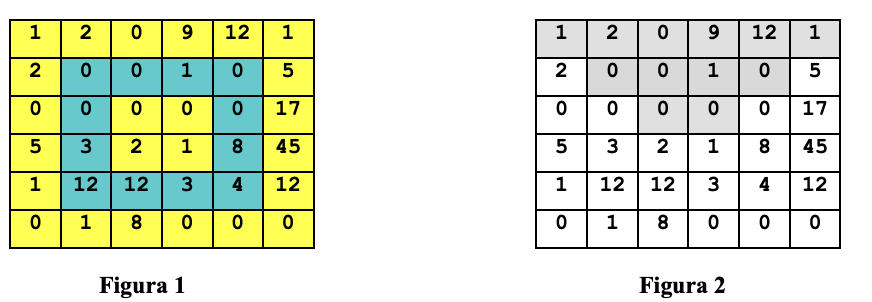
Dispozitivul conţine mai multe rame mobile (reprezentate în figură prin pătrate concentrice haşurate diferit), care se pot roti cu $90$, $180$, $270$ sau $360$ de grade spre stânga sau spre dreapta, modificând astfel modul de dispunere a numerelor înscrise pe butoanele dispozitivului. Pentru exemplul din $\text{Figura} \ 1$, avem un număr de $3$ rame, reprezentate în figură prin culori de fond diferite.
Bomba se dezamorsează dacă suma elementelor de pe prima linie (cea din nord) a fiecărei rame este maximă (zona haşurată din $\text{Figura} \ 2$). Convenim să numim această porţiune a tabloului zona de nord.

Cerinţă

Scrieţi un program care să determine suma elementelor din zona de nord a tabloului, atunci când ramele cifrului au fost aduse în poziţia ce dezamorsează bomba, precum şi configuraţia tabloului.

Date de intrare

Fişierul de intrare cifru.in conţine:
Pe prima linie numărul natural $N$, reprezentând numărul liniilor şi coloanelor tabloului.
Pe fiecare din următoarele $N$ linii se află câte $N$ numere naturale, separate prin spaţiu, reprezentând numerele înscrise pe butoanele dispozitivului.

Date de ieşire

Fişierul de ieşire cifru.out va conţine pe prima linie un număr natural $S$ reprezentând suma maximă posibil de obţinut în zona de nord a tabloului. Pe următoarele $N$ linii se vor afişa elementele tabloului obţinut prin rotaţia ramelor în poziţia ce dezamorsează bomba (câte $N$ elemente separate prin câte un spaţiu).

Restricţii şi precizări

• $1 \lt N \lt 101$
• Numerele înscrise pe butoanele cifrului sunt numere naturale între $0$ şi $1 \ 000$.
• O ramă este compusă din cel puţin $2$ linii şi $2$ coloane.
• Se garantează că, pentru fiecare ramă, suma maximă se poate obţine pe o singură latură.

Exemplu

cifru.in

5
5 1 1 1 4
5 0 0 0 2
5 1 0 2 2
5 2 3 4 2
7 3 3 3 8

cifru.out

36
7 5 5 5 5
3 4 3 2 1
3 2 0 1 1
3 0 0 0 1
8 2 2 2 4

Explicaţie

Cifrul din exemplu este compus din două rame. Prima ramă, cea exterioară, a fost rotită cu $90$ de grade spre stânga, iar a doua ramă a fost rotită cu $180$ de grade spre stânga sau spre dreapta.
Suma elementelor îngroşate este $36$, fiind cea mai mare sumă posibil de obţinut prin rotirea în toate modurile a celor două rame.