medalion

Rapunzel, frumoasa prinţesă cu păr blond, lung şi magic, se pregăteşte pentru nunta sa cu legendarul Flynn Rider. Cu ocazia acestui eveniment, el îi va dărui prinţesei un medalion unic pe care aceasta îl va purta în ziua nunţii.

Comanda pentru confecţionarea medalionului este preluată de un renumit bijutier al regatului care primeşte de la Flynn $k$ cutii (numerotate de la $1$ la $k$), fiecare cutie conţinând foarte multe cristale, identice ca valoare. Astfel, toate cristalele din prima cutie au valoarea $1$, toate cristalele din cea de-a doua cutie au valoarea $2$ şi aşa mai departe, astfel încât toate cristalele din ultima cutie au valoarea $k$. Bijutierul va monta cristalele pe o plachetă de aur de formă pătratică cu $n$ rânduri de cristale, pe fiecare rând fiind montate $n$ cristale unul lângă altul. Acesta ia pe rând câte un cristal din fiecare cutie, în ordinea: $1$, $2$, $3$, $\dots$, $k$, $1$, $2$, $3$, $\dots$, $k$, $1$, $2$, $3$, $\dots$ şi le aşează pe placheta de aur în formă de spirală. Spirala porneşte din centrul medalionului unde se montează primul cristal. Al doilea cristal se montează în dreapta primului, iar următorul cristal, mai jos, pe rândul imediat următor. Montarea cristalelor se continuă pe acelaşi rând, mergând spre stânga, apoi în sus până la rândul situat deasupra rândului pe care se montează primul cristal. Se procedează în continuare la fel, respectând regula de construire a spiralei: dreapta, jos, stânga, sus şi aşa mai departe.

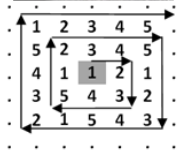
De exemplu, pentru $k = 5$, cristalele se montează pe medalion ca în desenul alăturat.

Cerinţă

1. Ştiind că bijutierul completează $n$ ($n$ număr natural impar) rânduri cu cristale pe placheta de aur, determinaţi cea mai mare sumă a valorilor tuturor cristalelor situate pe un rând al medalionului.
2. Determinaţi valoarea cristalului montat cu exact $p$ rânduri deasupra primului cristal montat în medalion şi plasat pe aceeaşi coloană cu acesta.

Date de intrare

Fişierul de intrare medalion.in conţine pe prima linie numerele naturale $k$, $n$, $p$ (în această ordine), cu semnificaţiile menţionate anterior. Valorile $k$, $n$, $p$ sunt separate prin câte un spaţiu.

Date de ieşire

Fişierul de ieşire medalion.out conţine pe prima linie un număr natural, ce reprezintă numărul determinat conform cerinţei $a)$, iar pe cea de-a doua linie un număr natural, determinat conform cerinţei $b)$.

Restricţii şi precizări

• $2 \leq k \leq 20$
• $3 \leq n \leq 301$
• $1 \leq p \leq 500 \ 000$
• numărul de cristale din fiecare cutie este suficient de mare pentru construirea medalionului;
• pentru rezolvarea corectă a cerinţei $1$ se acordă $40\%$ din punctajul fiecărui test, iar pentru rezolvarea corectă a cerinţei $2$ se acordă $60\%$ din punctajul fiecărui test

Exemplu

medalion.in

5 3 4

medalion.out

12
2

Explicaţie

$1.$ După montarea a $3$ rânduri de cristale se obţine configuraţia: Sumele valorilor cristalelor de pe aceste rânduri sunt:
$2 + 3 + 4 = 9$
$1 + 1 + 2 = 4$
$5 + 4 + 3 = 12$
Suma cea mai mare este $12$.
$2.$ Cristalul situat cu $4$ rânduri deasupra centrului medalionului, marcat în desenul alăturat, are valoarea $2$.