Ionuţ a învăţat la şcoală să lucreze cu numere mari. El are la dispoziţie un şir de numere naturale nenule. Din fiecare număr el şterge exact trei cifre, fără să schimbe ordinea cifrelor rămase, astfel încât să obţină cel mai mic număr natural nenul posibil. De exemplu, din numărul 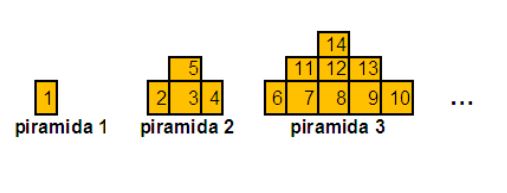 se obţine numărul , iar din numărul se obţine numărul . Înlocuind fiecare număr citit cu numărul obţinut prin operaţia de mai sus, Ionuţ obţine un nou şir şi scrie termenii acestuia pe feţele unor cuburi astfel: primele şase numere din şir le scrie pe primul cub şi îl notează pe acesta cu , următoarele şase numere din şir le scrie pe un alt cub pe care îl notează cu ş.a.m.d.
se obţine numărul , iar din numărul se obţine numărul . Înlocuind fiecare număr citit cu numărul obţinut prin operaţia de mai sus, Ionuţ obţine un nou şir şi scrie termenii acestuia pe feţele unor cuburi astfel: primele şase numere din şir le scrie pe primul cub şi îl notează pe acesta cu , următoarele şase numere din şir le scrie pe un alt cub pe care îl notează cu ş.a.m.d.
Aceste cuburi au fost distribuite în piramide după modelul din figura de mai sus. Piramidele au fost numerotate cu numere naturale consecutive. Piramida cu numărul de ordine este formată numai din cubul cu numărul de ordine şi are un singur nivel, piramida cu numărul de ordine are pe primul nivel cuburile şi iar pe ultimul nivel cubul ş.a.m.d.
Două niveluri alăturate în cadrul unei piramide diferă prin exact două cuburi. Primul nivel al unei piramide conţine cu două cuburi mai mult decât primul nivel al piramidei precedente. Piramida se consideră completă dacă pe ultimul nivel are un singur cub.
Cerință
Scrieţi un program care citeşte numerele naturale nenule şi , apoi cele numere naturale ce fac parte din şirul iniţial, şi determină:
- Numărul de piramide complete construite de Ionuţ.
- Numerele scrise pe cuburile din primele piramide.
Date de intrare
Fişierul cuburi.in are două linii: prima linie conţine două numere naturale, şi , iar a doua linie conţine numere naturale. Pe fiecare linie a fişierului numerele sunt separate prin câte un spaţiu.
Date de ieșire
Fişierul cuburi.out are două linii: prima linie conţine numărul de piramide complete care au fost construite, iar a doua linie conţine toate numerele scrise pe cuburile ce formează primele piramide. Numerele sunt scrise separate prin câte un spaţiu, în ordinea apariţiei lor în şirul nou obţinut.
Restricții și precizări
- Se garantează că se pot construi cel puţin piramide complete.
- Cele numere naturale de pe a doua linie a fişierului de intrare au minimum patru cifre şi maximum cifre.
- Se acordă din punctajul acordat problemei pentru rezolvarea corectă doar a primei cerinţe.
Exemplu
cuburi.in
31 2
18250 9280 18250 953805 20800 6040065 24208 4405 8794 1720 98886 96400 45544 8560056 36055 60400 80200 11560 36475 26992 68320 69400 20296 72640 34048 57700 66520 47440 91232 26080 90280
cuburi.out
2
10 2 10 305 20 4005 20 4 4 1 86 40 44 5005 30 40 20 10 34 22 20 40 20 20 30 50 20 40 12 20
Explicație
Primele numere se găsesc pe cubul ce formează prima piramidă, următoarele de numere sunt scrise, în această ordine, pe feţele cuburilor ce alcătuiesc a doua piramidă.
Observaţie: în acest tabel, datorită spaţiului insuficient, numerele nu apar scrise pe exact două linii, ca în fişierele de intrare/ieşire.