Deși nu obișnuiește să deseneze, Adrian are o pasiune inedită: îi place să schițeze pe hârtie orașe imaginare... mai exact cum ar arăta acestea văzute de sus. În acest an, de ziua lui a primit cadou un pergament! Normal că menirea acestuia va fi ca Adrian să deseneze pe el schița celui mai mare oraș pe care și l-a imaginat până acum.
Pergamentul are lățimea unei coli de hârtie, însă lungimea sa este neașteptat de mare. De asemenea, pergamentul este împărțit în pătrate astfel încât pe lungime se află exact pătrate iar pe lățime se află exact pătrate. Astfel, Adrian are la dispoziție exact pătrate pe care le poate colora.
El decide să coloreze doar străzile orașului, deoarece nu are timp de mai mult și plănuiește să folosească două tipuri de străzi:
- Străzi orizontale
- Vor fi desenate ca o secvență continuă de pătrate albastre.
- Pe fiecare rând de la la se va afla exact o stradă orizontală. Deci, la final vor fi exact străzi orizontale.
- Fiecare stradă se desfășoară pe un singur rând.
- Lungimea fiecărei străzi va fi de minim un pătrat și de maxim pătrate și este egală cu numărul de pătrate ce o compun.
- Strada poate începe pe oricare pătrat de pe rând și poate avea orice lungime cât timp nu depășește limitele pergamentului.
- Străzi verticale
- Vor fi desenate ca o secvență continuă de pătrate roșii.
- Adrian va desena exact străzi verticale, desfășurate pe una dintre coloanele de la la .
- Pe o coloană pot exista mai multe străzi verticale cu condiția să nu se suprapună. Nu este obligatoriu să existe străzi verticale pe toate coloanele.
- Lungimea fiecărei străzi va fi de minim un pătrat și de maxim pătrate și este egală cu numărul de pătrate ce o compun.
- Strada poate începe pe oricare pătrat de pe coloană și poate avea orice lungime cât timp nu depășește limitele pergamentului.
La final, Adrian observă că anumite pătrate au devenit mov, deoarece fac parte atât dintr-o stradă verticală cât și din una orizontală, deci au fost colorate atât cu roșu cât și cu albastru. Adrian este fascinat de apariția acestora și vrea să știe câte pătrate mov sunt în desenul său. Fiind prea obosit să le numere, vă roagă pe voi să-l ajutați.
Cerință
Cunoscând numerele , , , precum și poziționarea celor străzi orizontale și a celor străzi verticale, să se determine numărul de pătrate mov din pergament.
Date de intrare
Pe prima linie a fișierul de intrare pergament.in se află trei numere naturale separate prin câte un spațiu, , , , cu semnificația din enunț.
Pe a doua linie se află patru numere naturale separate prin câte un spațiu, , , , .
Pe a treia linie se află două numere naturale și , unde reprezintă coloana pătratului de început al străzii orizontale de pe rândul 1, iar reprezintă lungimea acesteia.
Datele următoarelor străzi se vor calcula prin formulele de mai jos, unde reprezintă coloana pătratului de început al străzii orizontale de pe rândul (), iar reprezintă lungimea acesteia:
Pe următoarele linii se află câte trei numere naturale , și , unde reprezintă coloana pe care se află strada verticală, reprezintă rândul pe care se află pătratul de început al străzii, iar reprezintă lungimea străzii.
Date de ieșire
În fișierul de ieșire pergament.out se va afla un singur număr natural ce reprezintă numărul de pătrate mov din desenul lui Adrian.
Restricții și precizări
- Rândurile sunt numerotate de la la , iar coloanele sunt numerotate de la la .
- Pentru 40 de puncte, .
- Pentru alte 30 de puncte, .
- Pentru alte 30 de puncte, nu există condiții adiționale.
Exemplu
pergament.in
6 3 2
1 1 1 1
1 2
2 2 4
1 4 3
pergament.out
3
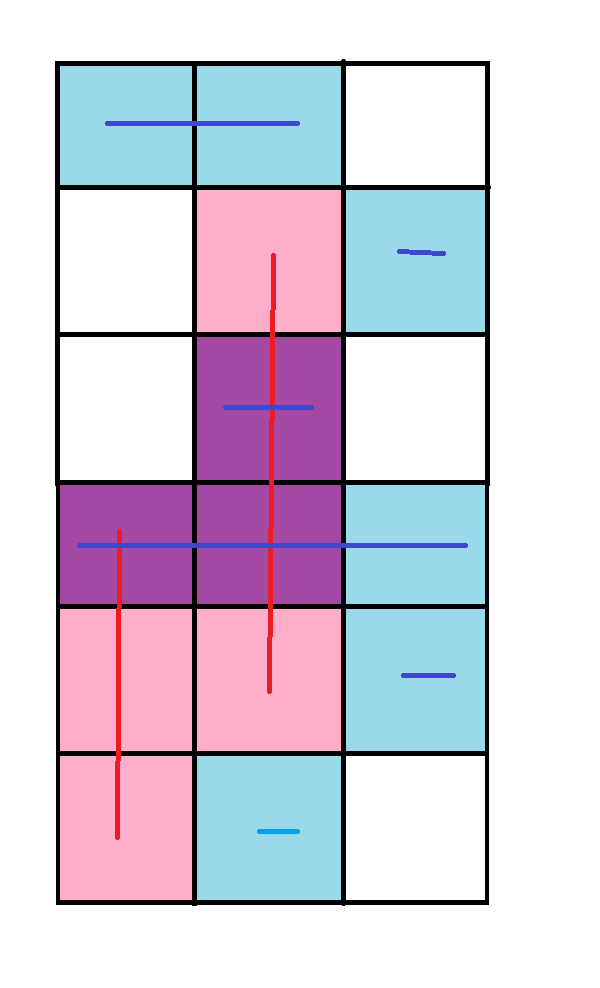
Imaginea alăturată reprezintă pergamentul desenat de Adrian din exemplu.
Conform formulelor, vom avea următoarele străzi orizontale:
- Linia 1: și
- Linia 2: și
- Linia 3: și
- Linia 4: și
- Linia 5: și
- Linia 6: și
Se observă că există exact 3 pătrate mov.